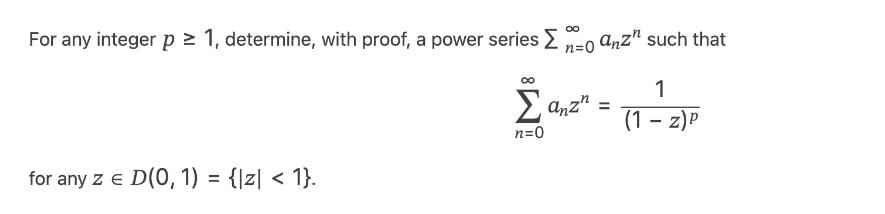
For any integer p 1, determine, with proof, a power series n=0 azn such that for any z = D(0, 1) = {|z| < 1}. 1 anz" = (1 - z)P n=0 Q2 (20 points) A function f (z) is analytic if there exists a power series > for any z = D(O, R) = {|z| < R}. Let f (z) be an analytic function such that n=0 anzn with positive radius of convergence R such that f (z) = n=0 anzn " (z) = f (z) Vz = D(O, R). Prove that there exist , B = C such that f(z) = sinh(z) + cosh(z) for any z = D(O, R). Q3 (20 points) (1) Determine, with proof, a degree 3 polynomial P(z) such that cos(3z) = P(cos(z)) for any z = C. (2) Prove that for any n 1 there exists a polynomial Pn(z) of degree n such that cos(nz) = P(cos(z)) for any z = C. Q4 (20 points) Determine whether there exists an analytic function f (z) defined in D(O, R) with f(n) (0) = (n!) for any n 1. Q5 (20 points) (1) Prove that three points in the complex plane Z1, Z2, Z3 are vertices of an equilateral triangle if and only if where w = e2i/3 is a third root of unity. Z + Zw + Z3w = 0, (2) A (counterclockwise) rotation of angle & and center p is the map R : C C R(z) = ela (z - p) + p. Consider three rotations R1, R2, R3 of angle 2/3 (note that they may not have the same center!) Show that if the composition 0 R1 R2 R3 is the identity map, then the three centers of rotation are vertices of an equilateral triangle.