Question: For m > 1, show that the m-step method Wi+1 = Wi+1-m +h (bmf(ti+1, Wi+1) + bm-1f (ti, wi) + . + bof (ti+1-m,

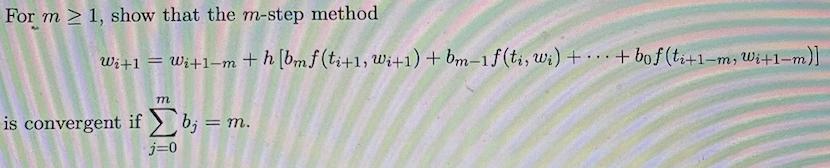
For m > 1, show that the m-step method Wi+1 = Wi+1-m

For m > 1, show that the m-step method Wi+1 = Wi+1-m +h (bmf(ti+1, Wi+1) + bm-1f (ti, wi) + . + bof (ti+1-m, Wi+1-m)] %3D m is convergent if b; = m. j=0

Step by Step Solution

★★★★★

3.36 Rating (149 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (2 attachments)

6364bf963e43f_239587.pdf

180 KBs PDF File

6364bf963e43f_239587.docx

120 KBs Word File

Students Have Also Explored These Related Mathematics Questions!

Show that h = 1.06 x 10-34 J s = 6.59 x 10-16 eV s

Show that the difference method w0 = , wi+1 = wi + a1f (ti ,wi) + a2f (ti + 2,w1 + 2f (ti ,wi)), For each i = 0, 1. . . N 1, cannot have local truncation error O (h3) for any choice of constants a1,...

Show that if a convergent series contains only a finite number of negative terms, then it is absolutely convergent.

Many enzyme-catalyzed reactions are consistent with a modified version of the Michaelis-Menten mechanism in which the second step is also reversible. (a) For this mechanism show that the rate of...

A tape recorder has a speed control system so that H(s) = 1 with negative feedback and L(s) = Gc(s)G(s) = K / s(s + 2)(s2 + 4s + 5). (a) Sketch a root locus for K, and show that the dominant roots...

'Consider once again the case of univariate missing data MAR for two bivariately normal variables, where the first variable, X1; is completely observed, and m observations (for convenience, the first...

5.39 (Examination question, University of Nottingham.) The EM algorithm is to be used as an alternative to the Newton-Raphson method for maximising the likelihood of Exercise 3.21 by imputing the...

A DLM for the univariate series yt is given by yt = F t + t where t N(0v), and t = Gt 1+ twhere t N(0vW)withtheusual conditional independence assumptions. All model parameters FvGW are known and...

For Eqs. (536) show that the principal stresses are given by i V2nr cos 2 ( 1 + sin KI ( 1-sin cos (plane stress) IV -r vA7 cos 2 (plane strain)

(Feller14) A large number, N, of people are subjected to a blood test. This can be administered in two ways: (1) Each person can be tested separately, in this case N test are required, (2) the blood...

Find the antiderivative F of f that satisfies the given condition. Check your answer by comparing the graphs of fand F. F(x) = 2e* - 8x, F(0) = 3 F(x) =

Final Exam 12. NuCo uses the periodic method and has the following account balances: Purchase Returns, $17,000; Beginning Inventory, $4,000; Purchases, $193,000; Freight-In, $11,000; and Accounts...

You have now worked with both CSV files and JSON files. Certainly JSON files are more versatile, as they can represent a wider variety of data than a simple spreadsheet can. But a lot of data in the...

Your company has a Microsoft 365 E5 subscription. You need to identify vulnerable certificates on the company's devices. Which Vulnerability Management feature in Microsoft Defender for Endpoint...

The gra a quadratic function with vertex (0, 1) is shown in the Find the unge and the domain. 10 8 -2 24 6 8.10 Write the range and domain using interval notation. (a) range: (0,0) [0,0] (0,0)

Consider the equation z16 (1+ 3i). Find the value of z which satisfies this equation and which has the second smallest positive argument 0,0

Marketing would be classified as an upstream activity in the value chain of a merchandising firm. Select one: a. True b. False

What are the typical record-at-a-time operations for accessing a file? Which of these depend on the current file record?

Using software, conduct the analyses described in this chapter for the student survey data (Table 8.3). Table 8.3: Alcohol, Cigarette, and Marijuana Use for High School Seniors Marijuana Use...

Identify loglinear models that correspond to the logit models, for a

The response functions F(p) have asymptotic covariance matrix V F . Derive the asymptotic covariance matrix of the WLS model parameter estimator b and the predicted values F = Xb.

Examine the test statistic used in testing a population proportion. Why is it impossible to test the hypothesis that the population proportion equals zero using such a test statistic? Try to...

The Oasis Chemical Company develops and manufactures pharmaceutical drugs for distribution and sale in the United States. The pharmaceutical business can be very lucrative when useful and safe drugs...

Discuss the two types of statistical errors that can occur when a hypothesis is tested. Illustrate what you mean by using a business example for each.