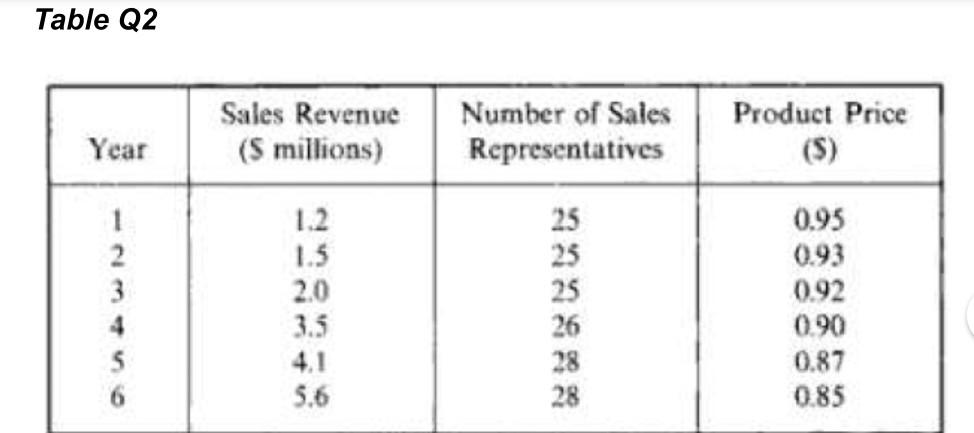
Forecasting is predicting or estimating the future value of a variable. Time-series analysis, one of three categories in forecasting techniques, is based on the idea that data describing past demand can be used to predict future demand. Linear Regression Analysis is used to define a functional relationship between two or more correlated variables. This relationship is usually developed from observed data where one or more values (the independent variables) are used to predict another (the dependant variable). Simple Linear Regression also known as Causal Linear Regression may refer it as Time-Series Linear Regression or Trend Regression. Linear regression is used for both time-series forecasting and causal relationship forecasting Consider the linear regression equation Y = a + bx, where Y is the dependent variable, X is the independent variable, a is the vertical axis intercept, and b is the slope of the straight line. The values of constant a and b are obtained as follows: ds - xy, -(x) y 2-(x)? 21 Where x is the independent variable data, y is the dependent variable data, and n is the total number of observations. Using the above values of a and b in the linear regression equation (Y= a + bx), Y can be estimated for future value of X. If data are a time series, the independent variables is the time period and the dependent variable is the variable to be forecasted. Such relationship, known as time series linear regression or trend line, is expressed as; Y= a + bT where Tis the time period. The coefficient of correlation (1) is a relative measure of the relationship between the dependent variable y and the independent variable x, computed as follows; H Xy - ) VnEx-(x)][-() where -Isrs +1. A perfect relationship exisis, when r = +1. The coefficient of determination is the square of the coefficient of correlation, a measure of the proportion of variance in the dependent variable y that can be explained by the independent variable x. Note that, Osr 31 Example, if + = 0.9, the independent variable explains 90% of the variation in the dependent variable. Consider a case on a manufacturing company is having the following financial data that represents the projected performance of the company. The data in Table Q2 represent the relationship between the dependent variables Sales Revenue in millions of dollars - and the independent variables - Number of Sales Representatives and Product Price. - Table Q2 Product Price Sales Revenue (5 millions) Number of Sales Representatives Year 1.2 1 2 3 1.5 2.0 3.5 4.1 5.6 25 25 25 26 28 28 0.95 0.93 0.92 090 0.87 0.85 S 6 a) If the company intends to increase the number of sales representatives to 30, use causal linear regression to forecast next year's sales revenue. b) If the company plans to decrease the product price to $0.82 next year, forecast next year sales revenue using causal linear regression. c) Forecast next year's sales revenue using time series linear regression with time as the independent variable. d) Determine the most reliable result of part (i), (ii) and (iii) using the coefficient of determination