Free fall of a Bungee Jumper using Bisection algorithm

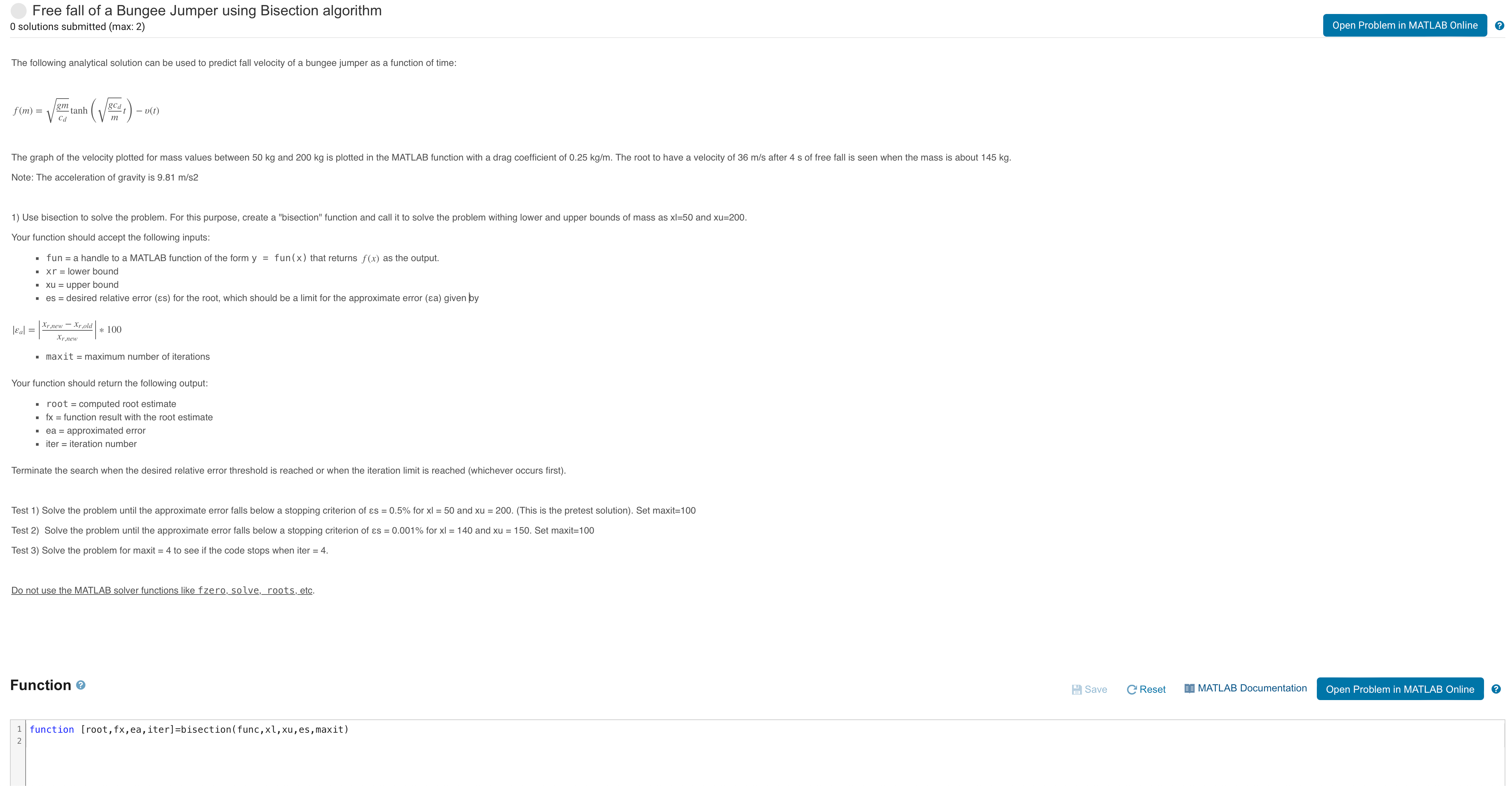
The following analytical solution can be used to predict fall velocity of a bungee jumper as a function of time:

$f(m)=\sqrt[\phantom{2}]{\frac{gm}{c_d}}tanh(\sqrt[\phantom{2}]{\frac{g{c}_d}{m}}t)-v(t)$

The graph of the velocity plotted for mass values between $50kg$ and $200kg$ is plotted in the MATLAB function with a drag coefficient of $0\mathrm{.}25k\frac{g}{m}.$ The root to have a velocity of $36\frac{m}{s}$ after $4s$ of free fall is seen when the mass is about $145kg.$

Note: The acceleration of gravity is $9\mathrm{.}81\frac{m}{s}2$

Use bisection to solve the problem. For this purpose, create a "bisection" function and call it to solve the problem withing lower and upper bounds of mass as $xl=50$ and $xu=200.$

Your function should accept the following inputs:

fun $=$a handle to a MATLAB function of the form $y=$ fun $(x)$ that returns $f(x)$ as the output.

$xr=$ lower bound

$xu=$ upper bound

es $=$ desired relative error $(s)$ for the root, which should be a limit for the approximate error $($ a$)$ given by

$|{}_a|=|\frac{x_{r,\text{n}\text{e}\text{w}}-x_{r,\text{o}\text{l}\text{d}}}{x_{r,\text{n}\text{e}\text{w}}}|*100$

maxit $=$ maximum number of iterations

Your function should return the following output:

root $=$ computed root estimate

$fx=$ function result with the root estimate

ea $=$ approximated error

iter $=$ iteration number

Terminate the search when the desired relative error threshold is reached or when the iteration limit is reached $($whichever occurs first$).$

Test $1)$ Solve the problem until the approximate error falls below a stopping criterion of $s=0\mathrm{.}5\%$ for xl $=50$ and $xu=200.($This is the pretest solution$).$ Set maxit$=100$

Test $2)$ Solve the problem until the approximate error falls below a stopping criterion of $s=0\mathrm{.}001\%$ for $xl=140$ and $xu=150.$ Set maxit$=100$

Test $3)$ Solve the problem for maxit $=4$ to see if the code stops when iter $=4.$

Do not use the MATLAB solver functions like fzero, solve, roots, etc.

I ONLY HAVE ONE CHANCE TO SUBMIT. PLEASE FOLLOW THE INSTRUCTIONS AND CHECK THE ASSESSMENT BELOW. ASSESSMENT SHOWS THINGS OUR TUTOR WIILL CHECK!