From Differential Equations, 4th Edition, by Paul Blanchard, Robert Devaney and Glen Hall

Lab 1.4

State: Florida

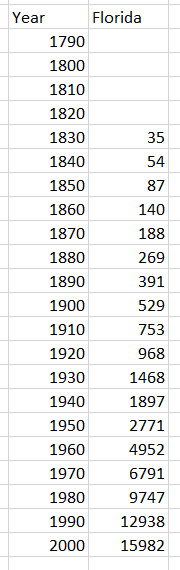
Your report should address the following items: 1. Using an exponential growth model, determine as accurate a prediction as possible for the population of your state in the year 2010. How much does your prediction differ from the prediction that comes from linear extrapolation using the populations in 1990 and 2000? To what extent do solutions of your model agree with the historical data? 2. Produce a logistic growth model for the population of your state. What is the carrying capacity for your model? Using Eulers method, predict the population in the years 2010 and 2050. Using analytic techniques, obtain a formula for the population function P(t) that satisfies your model. To what extent do solutions of your model agree with the historical data? 3. Comment on how much confidence you have in your predictions of the future populations. Discuss which model, exponential or logistic growth, is better for your data and why (and if neither is very good, suggest alternatives).

Year Florida 1790 1800 1810 1820 1830 35 1840 54 1850 87 1860 1870 1880 140 188 269 391 1890 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 529 753 968 1468 1897 2771 4952 6791 9747 12938 15982 2000 Year Florida 1790 1800 1810 1820 1830 35 1840 54 1850 87 1860 1870 1880 140 188 269 391 1890 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 529 753 968 1468 1897 2771 4952 6791 9747 12938 15982 2000