From the data given as an attachment in this question, my professor wants us to show how b is .7054 and power (1 - b) is .2946. (Note that this example shows a one-tailed test.)

The answer here should be power = .2946 which is given, he just wants us to show HOW these answers came to be. Of course I am not looking for you to provide me all of the answers, because I really want to understand! I am just so confused on where to begin. Can you please further assist me on what formulas to use in order of when I should use them? Any information regarding how this works and what all this even means? Please just guide me in the right direction. I hope this question makes sense and is acceptable.

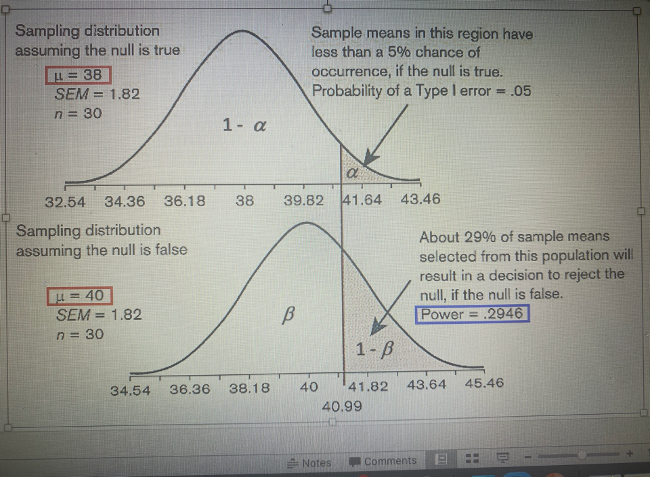
Sampling distribution assuming the null is true Sample means in this region have less than a 5% chance of LL = 38 occurrence, if the null is true. SEM = 1.82 Probability of a Type I error = .05 n = 30 1 - a 32.54 34.36 36.18 38 39.82 41.64 43.46 Sampling distribution assuming the null is false About 29% of sample means selected from this population will result in a decision to reject the L = 40 SEM = 1.82 null, if the null is false. Power = .2946 n = 30 1 - B 34.54 36.36 38.18 40 41.82 43.64 45.46 40.99 Notes Comments