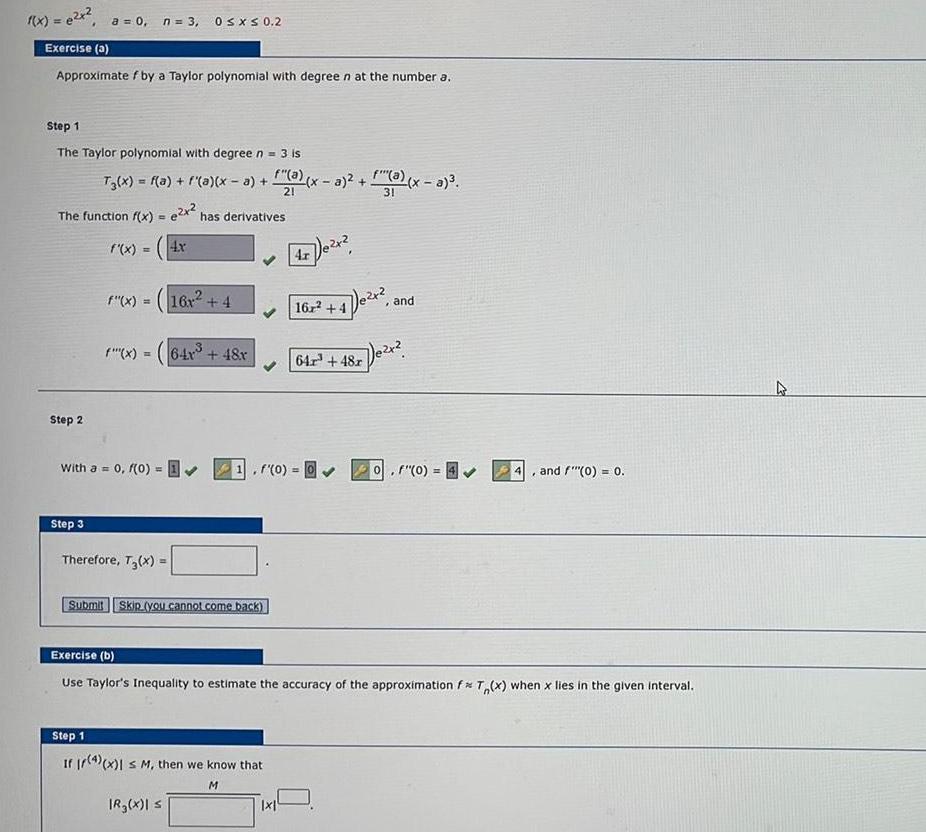
f(x) = ex, a = 0, n = 3, 0 x 0.2 Exercise (a) Approximate f by a Taylor polynomial with degree n at the number a. Step 1 The Taylor polynomial with degree n = 3 is T3(x) = f(x) + "(a)(x-2)+(a)(x-3)2 + (a)(x-a). 31 21 The function f(x)=2x2 has derivatives f'(x). = 4x 4r Step 2 f"(x) = 16r2+4 16x+4 , and f'"'(x)== 64x +48x 64x+48xex With a = 0, f(0) = 1, f'(0) = 0 and ""(0) = 0. Step 3 Therefore, T3(x) Submit Skip (you cannot come back) Exercise (b) Use Taylor's Inequality to estimate the accuracy of the approximation fx T(x) when x lies in the given interval. Step 1 If (4)(x) s M, then we know that M IR(x)| s 1x1