Gaussian Elimination in Matlab

In this problem we test the performance of the the naive Gaussian elimination procedure and compare it with the linear system solver implemented in Matlab (which uses scaled partial pivoting). As a test problem, we solve the system:

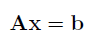
where A is the Vandermonde-matrix:

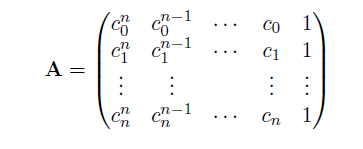
where c = [c₀,c_1,..., c_n] is a given vector. Since the main point of this problem is to compare the two algorithms, we choose a vector b which gives a known solution x. For example, if the solution is x = ones(n)=[1, 1, ... ,1], then the load vector is b = A ones(n).

Solve the above system with two different algorithms: The naive Gaussian elimination without pivoting, using the function naiv_gauss(A,b). Gaussian elimination with pivoting in Matlab, i.e., using the command x = A\b;

You should test it for the following 3 cases:

i) c = [0.2,0.4,0.6,0.8,1]^T

ii) c = [0.1, 0.2, 0.3, ..., 0.9. 1]^t

iii) c = [0.05, 0.10, 0.15, ..., 0.90, 0.95, 1]^T

Below is the MATLAB function naiv_gauss:

function x = naiv_gauss(A,b); n = length(b); x = zeros(n,1);

for k=1:n-1 for i=k+1:n xmult = A(i,k)/A(k,k); A(i,k) = xmult; for j=k+1:n A(i,j) = A(i,j)-xmult*A(k,j); end b(i) = b(i)-xmult*b(k); end end x(n) = b(n)/A(n,n); for i=n-1:-1:1 sum = b(i); for j=i+1:n sum = sum-A(i,j)*x(j); end x(i) = sum/A(i,i); end

Ax b