Given a bipartite graph G = (M, W, E) where |M| = |W| = n, Where the node names in M are {1, 2, . . . n}, and so are the nodes in W (M stands for Men and W stand for Women).

There are undirected edges between M and W. But, the degree of nodes in M are 1) The whole graph contains exactly n edges).

1. If in G each node in W has degree 1 or more, show that the graph is a perfect match.

2. If the graph is not a perfect match, we want to find the largest subset L from {1, 2, . . . , n} such that the subgrapgh induced by the Men in L and the Women in L constitutes a perfect match in the induced subgraph. Your algorithm should be linear time.

For example: if we have 2 men m1, m2 and 2 women w1, w2 and edges e1, e2 going from , . A subset L = {1}, since the only possible solution will be .

Example of the graph: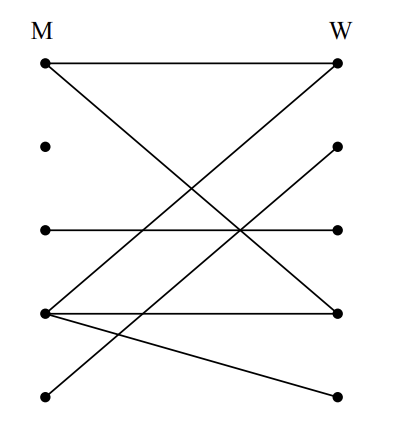

M W