We consider the Bipartite Matching Problem on a bipartite graph G = (V, E). As usual, we say that V is partitioned into sets X and Y, and each edge has one end in X and the other in Y. If M is a matching in G, we say that a node y Y is covered by M if y is an end of one of the edges in M. (a) Consider the following problem. We are given G and a matching M in G. For a given number k, we want to decide if there is a matching M in G so that (i) M has k more edges than M does, and (ii) every node y Y that is covered by M is also covered by M . We call this the Coverage Expansion Problem, with input G, M, and k. and we will say that M is a solution to the instance.

Give a polynomial-time algorithm that takes an instance of Cov- erage Expansion and either returns a solution M or reports (correctly)

that there is no solution. (You should include an analysis of the run- ning time and a brief proof of why it is correct.)

Note: You may wish to also look at part (b) to help in thinking about this.

Example. Consider Figure 7.29, and suppose M is the matching con- sisting of the edge (x1, y2). Suppose we are asked the above question

with k = 1. Then the answer to this instance of Coverage Expansion is yes. We can let M be the matching consisting (for example) of the two edges (x1, y2) and (x2, y4); M has one more edge than M, and y2 is still covered by M

(b) Give an example of an instance of Coverage Expansion, specified by G, M, and k, so that the following situation happens. The instance has a solution; but in any solution M

, the edges of M do

not form a subset of the edges of M .

(c) Let G be a bipartite graph, and let M be any matching in G. Consider the following two quantities. K1 is the size of the largest matching M so that every node y that is covered by M is also covered by M . K2 is the size of the largest matching M in G.

Clearly K1 K2, since K2 is obtained by considering all possible match- ings in G.

Prove that in fact K1 = K2; that is, we can obtain a maximum matching even if were constrained to cover all the nodes covered by our initial matching M.

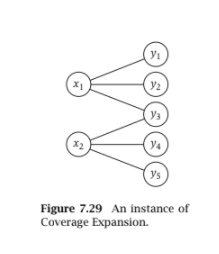
Y: X1 Y2 ya X2 14 ys Figure 7.29 An instance of Coverage Expansion