Given a graph G = (V, E) along with the cost di,j for each edge (i, j) E. Propose your algorithm to find a minimum-cost path subject to the condition that the hop-count number is no more than C, for some constant C [Hint: You can simply modify the Bellman-Fords algorithm]. Then, use your algorithm to find a minimum-cost path from node S to node 5 subject to the condition that the total hop-counts is no more than 3.

Edit: This problem just simply instructs the student to solve the minimum hop-count with Bellman-Ford's algorithm. C is any constant, so just solve the problem by figuring out the minimum hop-count with the specific algorithm.

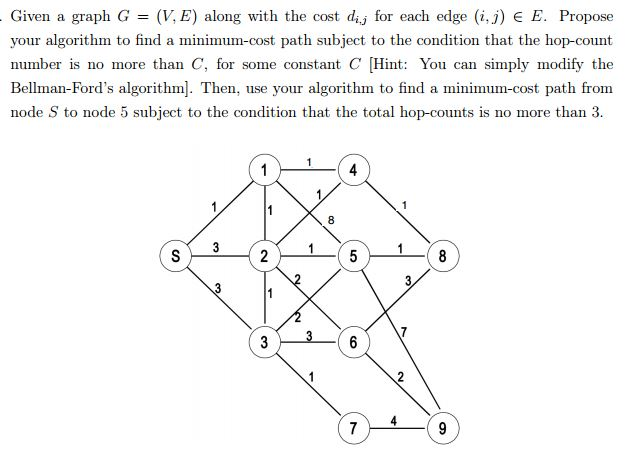
Given a graph G J (V, E) along with the cost dij for each edge (i ,j) E E. Propose your algorithm to find a minimum-cost path subject to the condition that the hop-count number is no more than C, for some constant C t: You can simply modify the Bellman-Ford's algorithm]. Then, use your algorithm to find a minimum-cost path from node S to node 5 subject to the condition that the total hop-counts is no more than 3