Question: Given: E ( R 1 ) = 0 . 1 3 E ( R 2 ) = 0 . 1 7 E ( sigma
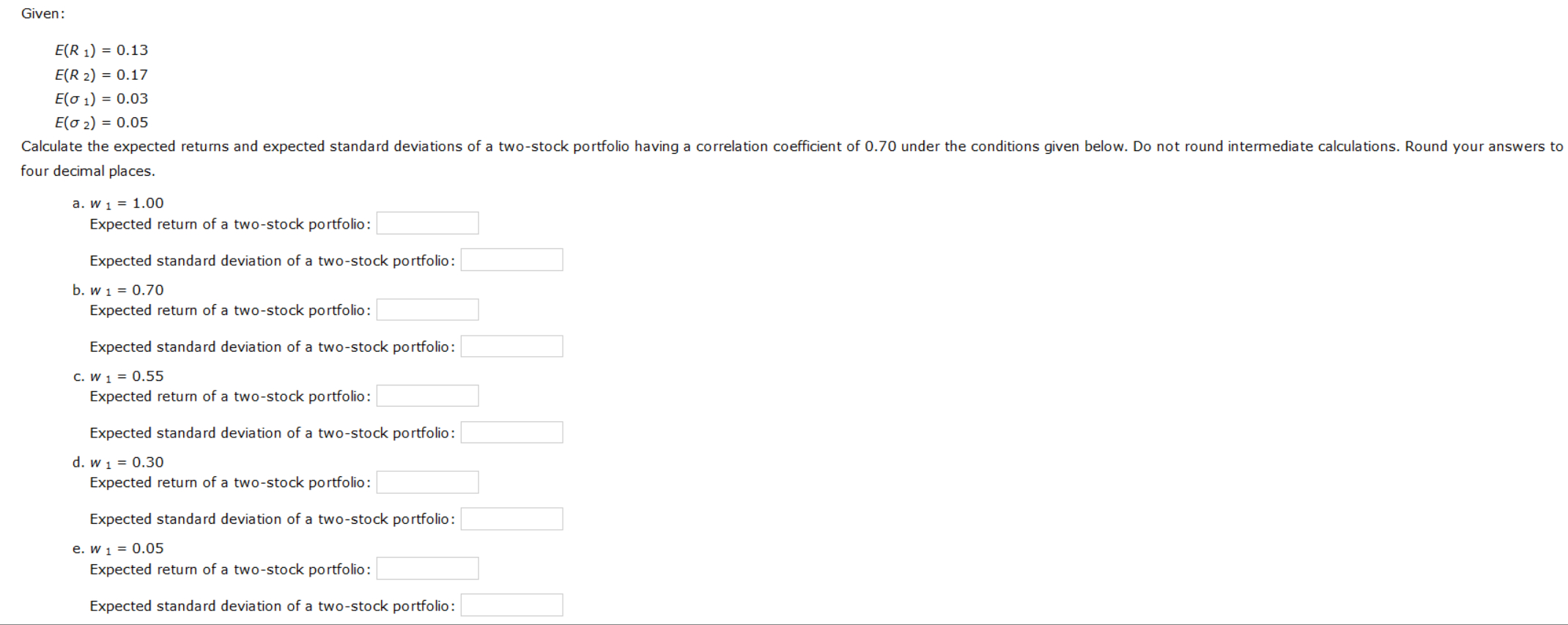
Given:
ER
ER
Esigma
Esigma
Calculate the expected returns and expected standard deviations of a twostock portfolio having a correlation coefficient of under the conditions given below. Do not round intermediate calculations. Round your answers to four decimal places.
w
Expected return of a twostock portfolio:
Expected standard deviation of a twostock portfolio:
w
Expected return of a twostock portfolio:
Expected standard deviation of a twostock portfolio:
w
Expected return of a twostock portfolio:
Expected standard deviation of a twostock portfolio:
w
Expected return of a twostock portfolio:
Expected standard deviation of a twostock portfolio:
w
Expected return of a twostock portfolio:
Expected standard deviation of a twostock portfolio:
Choose the correct riskreturn graph for weights from parts a through e when rij ; ;
Choose ONE of the following graphs that I have attached to the problem that are correct, do NOT make another graph. Look at other Chegg responses to similar to this question that have been marked mostly correct by other chegg users, PLEASE AND THANK YOU! Note, the standard deviation should be different for all, NOT the same. Please round to decimal places as well.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


