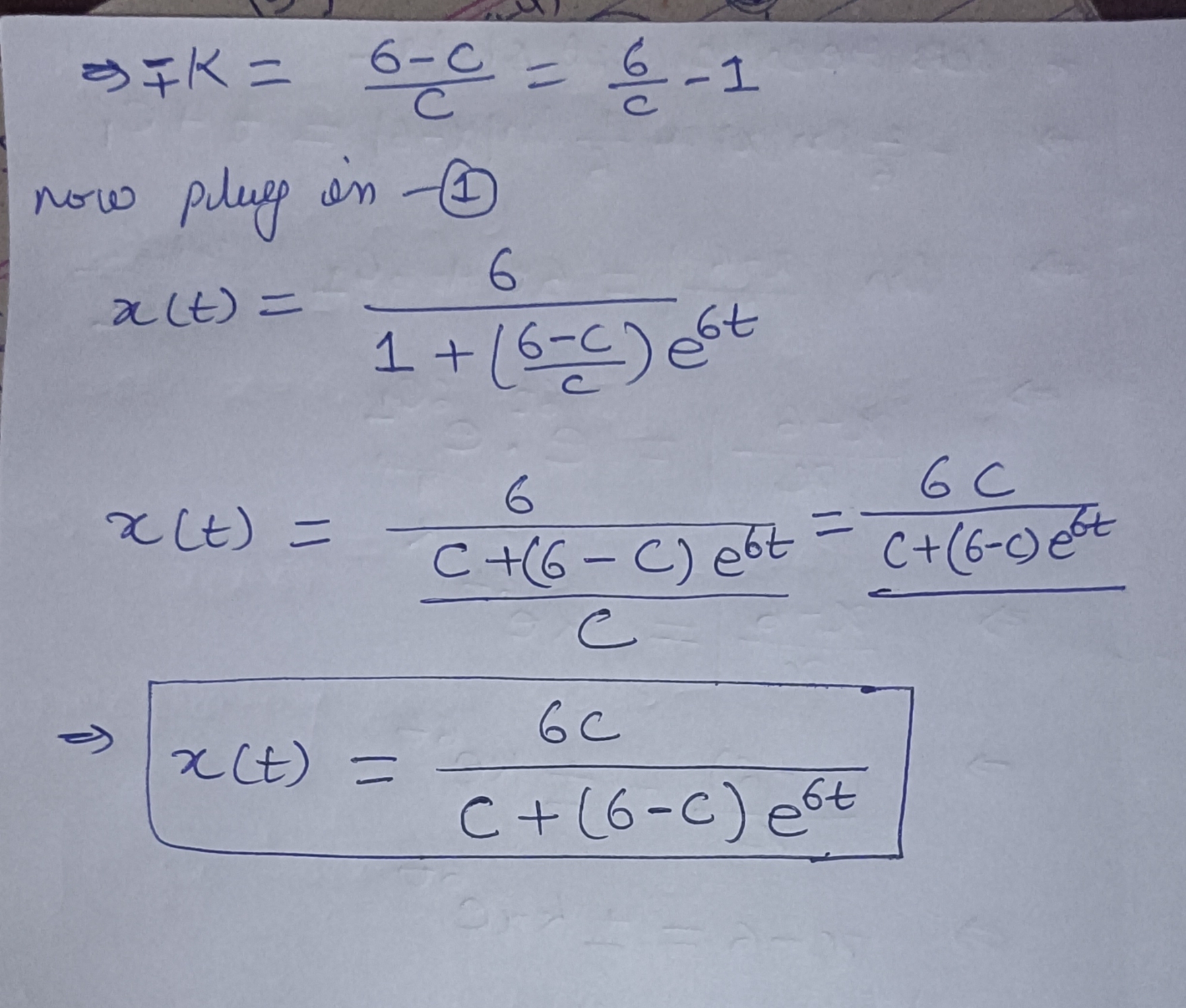
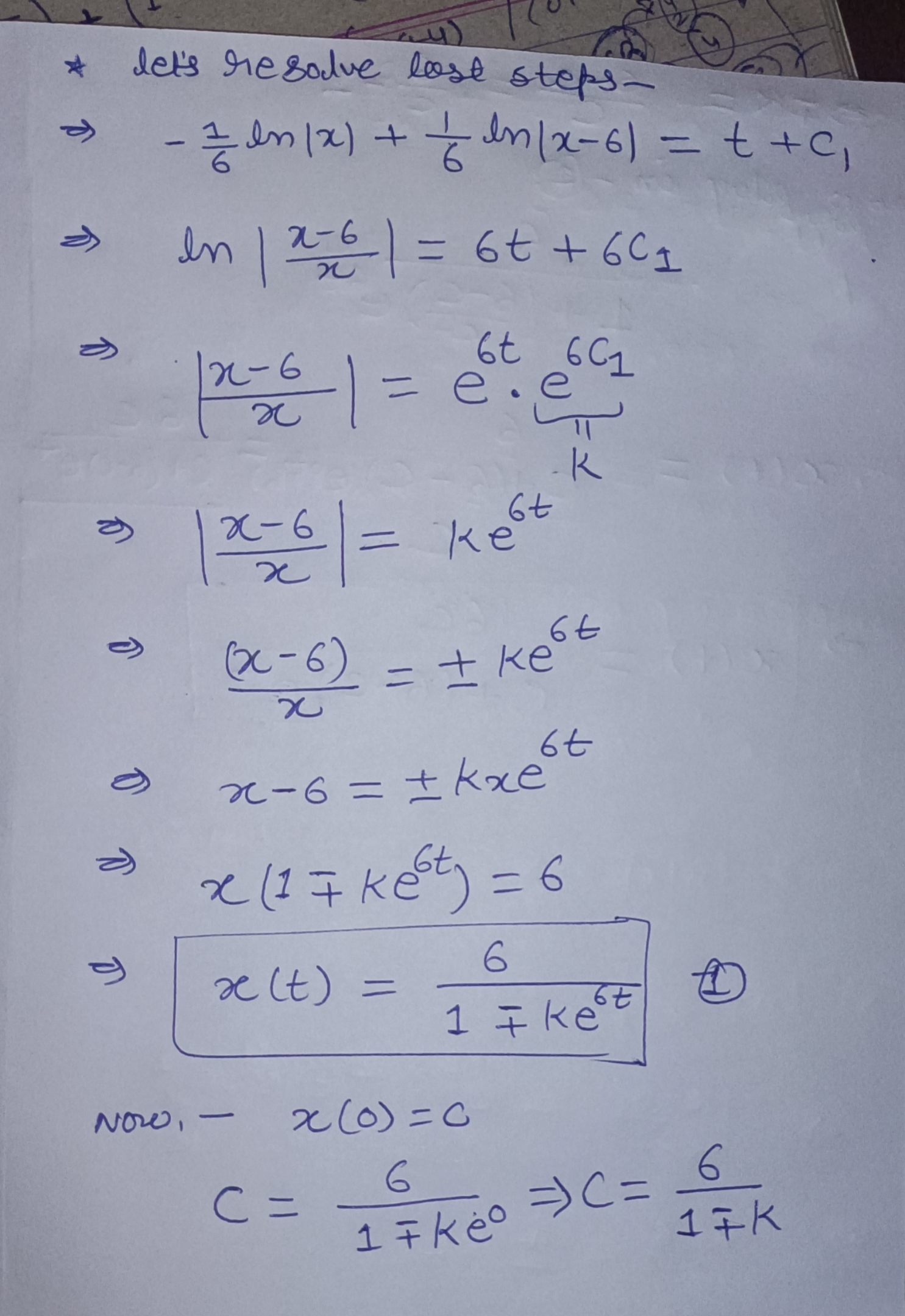
Given the autonomous differential equation d:E_ 2 Ew 6z, solve the equation dz == =@ dt to find the critical points of the given differential equation. Next, analyze the sign of f(z) to determine whether each critical point is asymptotically stable, semistable, or unstable. Place your answers in the table below. Smallest Critical Point Largest Critical Point o o) Stability | ' _| (Note: Indicate the stability of each point by typing one of the words stable, semistable, or unstable in the appropriate box.) Now, solve the differential equation explicitly for z(t) using the initial condition z(0) =C. Given the autonomous differential equation dz o Ew 6z, solve the equation dx = 0 dt to find the critical points of the given differential equation. Next, analyze the sign of f(x) to determine whether each critical point is asymptotically stable, semistable, or unstable. Place your answers in the table below. Smallest Critical Point Largest Critical Point 0] 6| Stability | stable | | unstable | (Note: Indicate the stability of each point by typing one of the words stable, semistable, or unstable in the appropriate box.) Now, solve the differential equation explicitly for z() using the initial condition z(0) =C. \f\f