Hello! Here is the homework problem I need help with. Thank you!

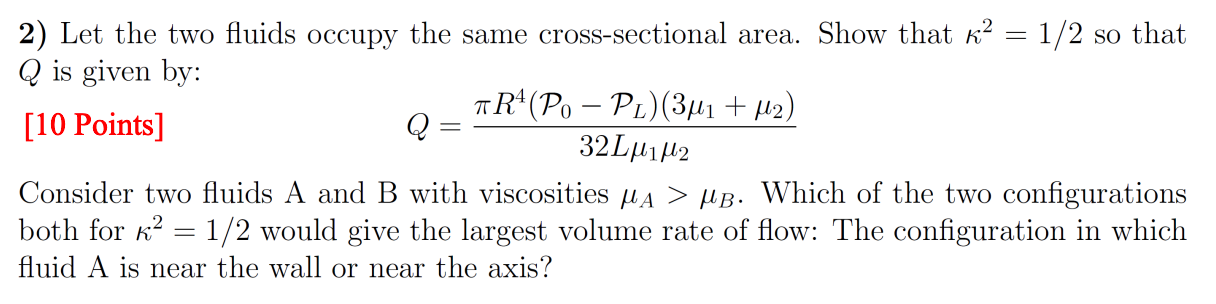
Consider steady laminar flow in a pipe of radius R of two immiscible incompressible Newtonian fluids. Fluid "l of viscosity Mi is located in the space r e [0, KR], while fluid 2 of viscosity M2 is located in the space r E (KR, R]. The interface between the two fluids at r = kR is assumed to be stationary. The flow is caused by a gradient in the modified pressure of Po PL over a distance L. It is assumed that the two fluids have the same density. 1) Show that the volume rate of flow Q is given by: [15 Points] aR4(Po Pl) K 8L 12 0 1 + Mi = 2) Let the two fluids occupy the same cross-sectional area. Show that k2 = 1/2 so that Q is given by: aR4(Po PL)(3u1 + M2) [10 Points] Q 32LMill2 Consider two fluids A and B with viscosities a > MB. Which of the two configurations both for k2 = 1/2 would give the largest volume rate of flow: The configuration in which fluid A is near the wall or near the axis? 3) Finally assume that the flow rates of the two fluids are equal. Obtain the resulting value of k as function of a = M2/M1. Show that [15 Points] if a = 3 KP if a # 3 1 2-V1+a 3-a Make a qualitative drawing of the expected velocity profiles for the two situations a 1