Hello , I need help with solving this assignment. Thank you

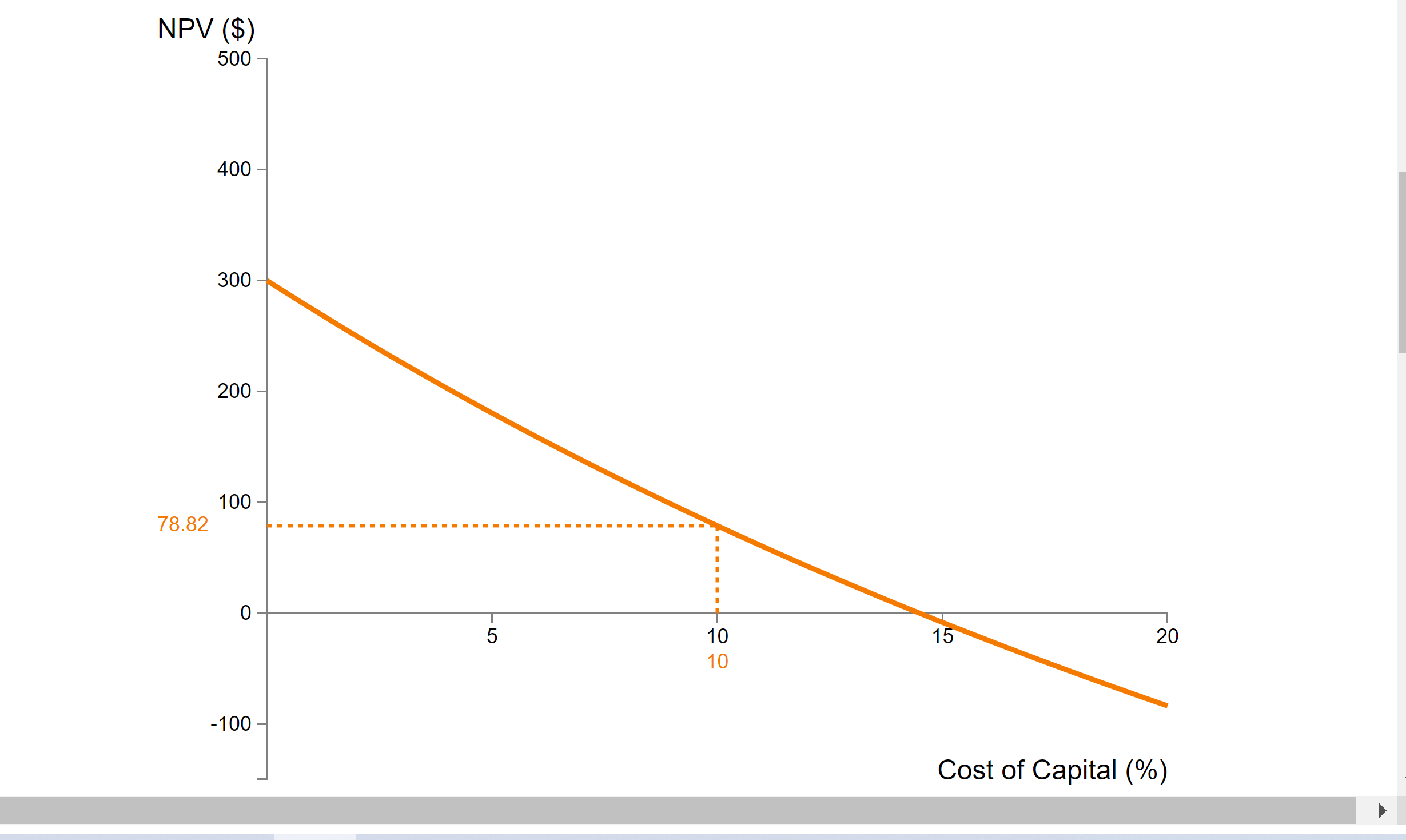
Conceptual Overview: Explore how the cost of capital affects the net present value of an investment project's decreasing cash flow. This graph shows the net present value of an investment with annual cash flows of $1,000,$500,$400,$300, and $100 as a function of different costs of capital (interest \%). Note that this cash flow returns declining amounts after the initial investment. Drag left or right on the graph to move the cursors to see the net present value (NPV) for different costs of capital. The point where the curve crosses the X-axis determines the internal rate of return (IRR). (Note: due to limited pixel resolution, it is sometimes difficult to get to that precise point.) NPV=CF0+t=1N(1+r)tCFt=$1,000+(1+0.1000)1$500+(1+0.1000)2$400+(1+0.1000)3$300+(1+0.1000)4$100=$78.82 1. What is the approximate IRR for the cash flow curve depicted? a. 5% b. 10% C. 15% d. 20% 2. When the cost of capital is less than a project's IRR, the NPV for the project is a. negative b. equals the project's IRR c. positive d. cannot be determined 3. If the cost of capital increases, the NPV for the project a. increases b. stays the same c. decreases d. cannot be determined 4. In the unrealistic situion in which the cost of capital were zero, the NPV of the project a. is the sum of the cash flows b. is the upper limit for the NPV of the project c. both of the above statements are correct d. neither of the first two statements is correct Conceptual Overview: Explore how the cost of capital affects the net present value of an investment project's decreasing cash flow. This graph shows the net present value of an investment with annual cash flows of $1,000,$500,$400,$300, and $100 as a function of different costs of capital (interest \%). Note that this cash flow returns declining amounts after the initial investment. Drag left or right on the graph to move the cursors to see the net present value (NPV) for different costs of capital. The point where the curve crosses the X-axis determines the internal rate of return (IRR). (Note: due to limited pixel resolution, it is sometimes difficult to get to that precise point.) NPV=CF0+t=1N(1+r)tCFt=$1,000+(1+0.1000)1$500+(1+0.1000)2$400+(1+0.1000)3$300+(1+0.1000)4$100=$78.82 1. What is the approximate IRR for the cash flow curve depicted? a. 5% b. 10% C. 15% d. 20% 2. When the cost of capital is less than a project's IRR, the NPV for the project is a. negative b. equals the project's IRR c. positive d. cannot be determined 3. If the cost of capital increases, the NPV for the project a. increases b. stays the same c. decreases d. cannot be determined 4. In the unrealistic situion in which the cost of capital were zero, the NPV of the project a. is the sum of the cash flows b. is the upper limit for the NPV of the project c. both of the above statements are correct d. neither of the first two statements is correct