Hello. Please help me solve these problems.

1)

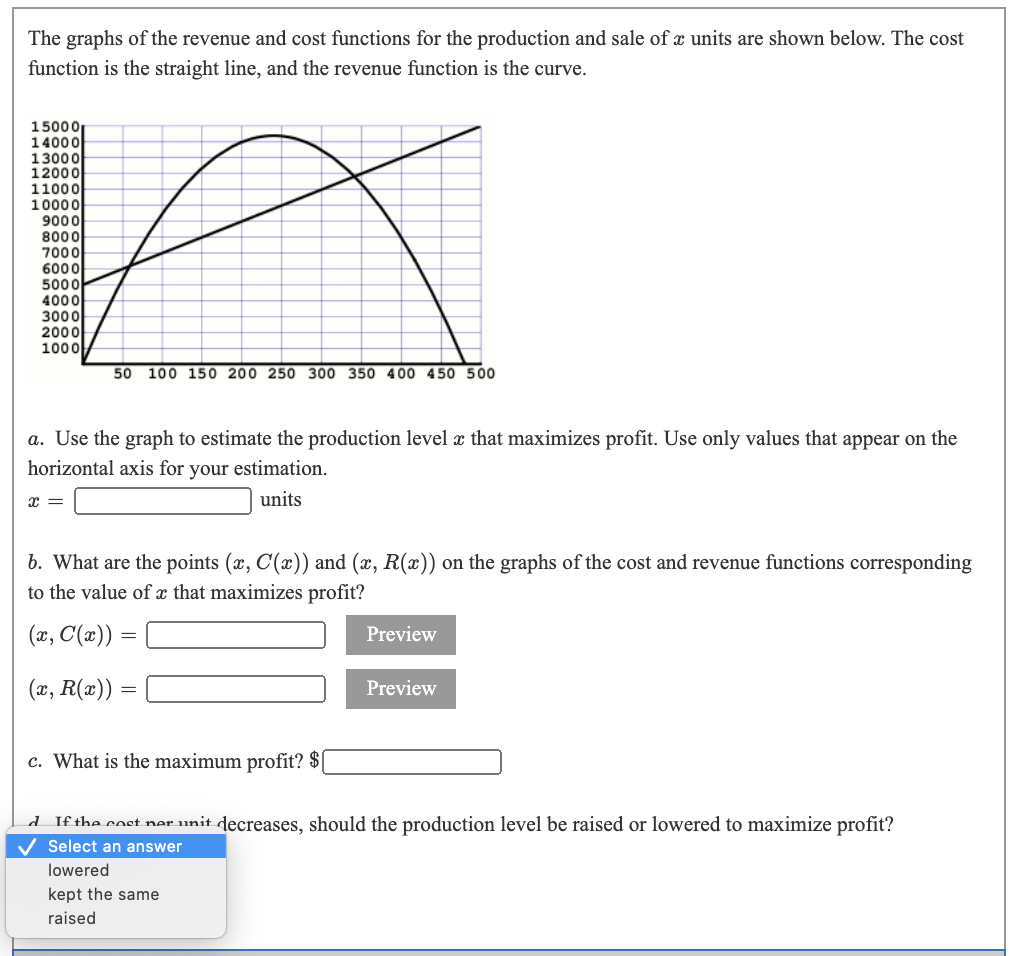
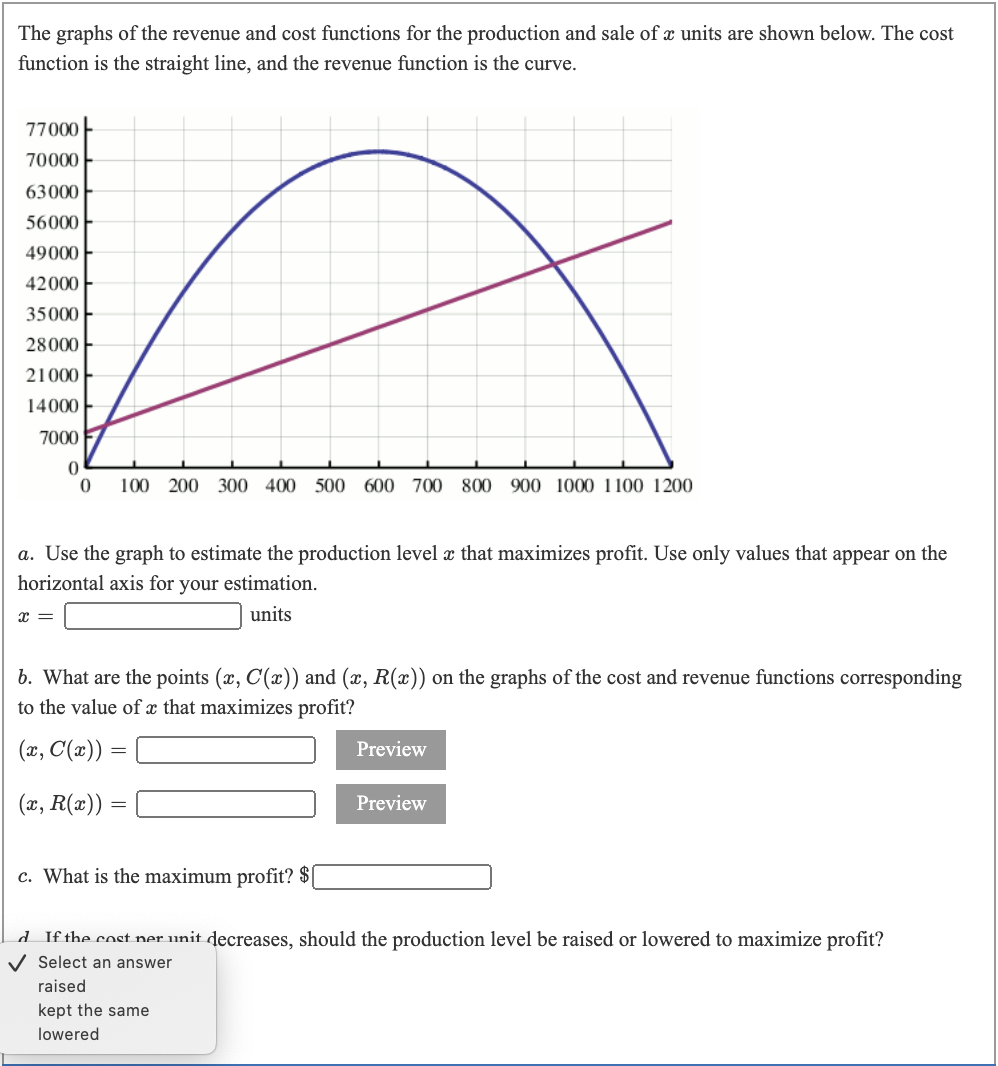
The graphs of the revenue and cost flmctions for the production and sale of 3: units are shown below. The cost function is the straight line, and the revenue function is the curve. 15000 14000 13000 12000 50 100 150 200 250 300 350 400 450 500 3. Use the graph to estimate the production level a: that maximizes prot. Use only values that appear on the horizontal axis for your estimation. .-:}m b. What are the points (at, 0(3)) and (:3, 12(3)) on the graphs of the cost and revenue Jnctions corresponding to the value of a: that maximizes prot? was = :1 em = :1 c. What is the maximum prot? 3:] - Mmases, should the production level be raised or lowered to maximize prot? J Select an answer lowered kept the same raised The graphs of the revenue and cost flmctions for the production and sale of :1: units are shown below. The cost function is the straight line, and the revenue function is the curve. 01(1) 200 30040:} 500 6110?\") son WOIOMIIOOIZOO (1. Use the graph to estimate the production level a: that maximizes prot. Use only values that appear on the horizontal axis for your estimation. .-:}m b. What are the points (1:, C(13)) and (:3, 12(3)) on the graphs of the cost and revenue mctions corresponding to the value of :2: that maximizes profit? mow = :1 won = :1 c. What is the maximum prot? 3:] Mummdecrcases, should the production level be raised or lowered to maximize prot? \\/ Select an answer raised kept the same lowered Sequoia Publishing Company plans to publish a vegetarian cookbook. The cost (in dollars) to produce :2: books 15: 0(3) = 2700 + 112:. The price-demand equation is: p = 70 0.15m. The revenue function is: 12(3) 2 70:1: 0.1532. :1. Compute the marginal cost and marginal revenue functions. Margmalcosw'tm) = :1 Margmanevenumm = :1 5. Use the marginal revenue mction to approximate the revenue for selling the 251st book. $:1- Get Help: AmeriB abe manufactures and sells rubber baby buggy bumpers. The price-demand equation is: p = 3100 8:: where p is the price (in dollars) at which a: rubber baby buggy bumpers can be sold. a. What is the demand if the price is $2650? The demandis :] bumpers. b. The cost to produce a: rubber baby buggy bumpers is given by 0(3) 2 600 + 11801: and the new revenue function is R(m) = 3(3100 8:13). How many rubber baby buggy bumpers should be manufactured and sold to maximize prot? AmeriBabe should produce and sell :] rubber baby buggy bumpers. Preview c. What price should AmeriBabe charge for each rubber baby buggy bumper to maximize prot? AmeriBabe should charge $:] per rubber baby buggy bumper. Get Heln: A company manufacturers and sells a: electric drills per month. The monthly cost and price-demand equations are 0(3) = 09000 + 40.: 23 p 200 30 0 _ :1: _ 5000 a. The production level that results in the maximum prot is :1 elecuicdrms b. The price that company should charge for each drill in order to maximize prot is :1 dollars