Help needed please. Must be in excel.

The bottom image is a figure reference.

And exercise 2.3.2 is for reference for 3.4.2

Example 2.3.2 DOES NOT NEED TO BE ANSWERED IT IS FOR REFERENCE

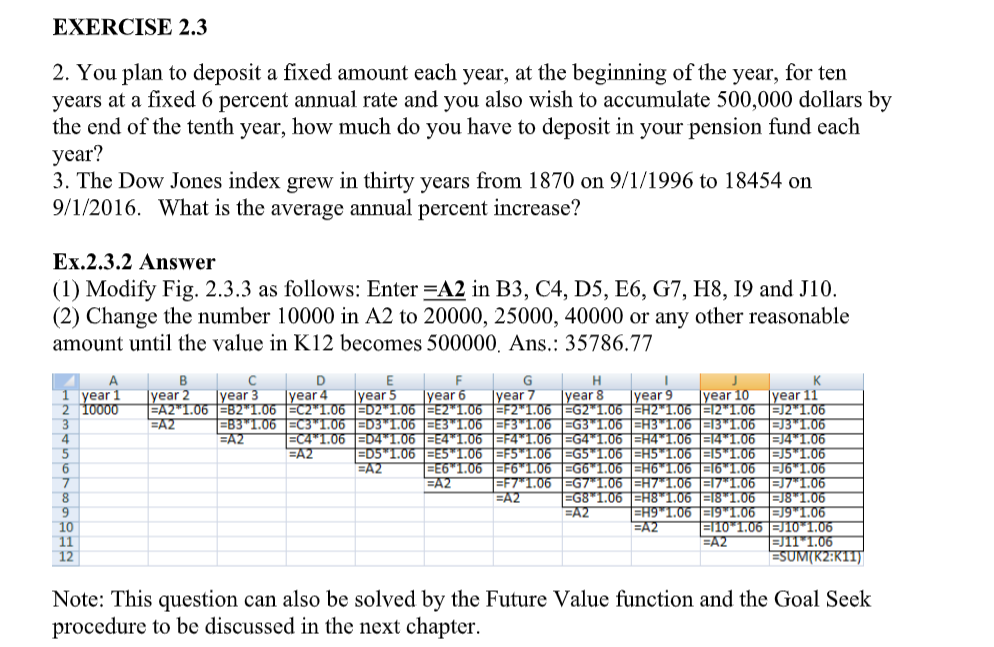
33 Goal 1000000 OK Cancel Fig. 3.4.2 (formula version of Fig. 3.4.1) D $5,526,59 30 10% 28 Annual Deposit 29 year 30 Annual Return 31 32 FV 33 Goal Fig. 3.4.3 $1,000,000.00 $1,000,000.00 EXERCISE 3.4 1. Mr. Kenneth borrowed 10,000 dollars at the beginning of last month. The monthly rate is 1%, and is charged at end of each month. Mr. Kenneth wishes to pay off his debt by paying $400 dollars each month, starting beginning of this month. How long will it take in order to pay off the entire debt? (Refer to Figure3.3.8 for timing of payments.) 40 2. Use Goal Seek to redo Exercise 2.3.2. Answer Exl.: Use PMT function and use Goal Seek. Set B5 to -400 by changing B3. Goal Seek Status ? X Booki 1 Loan 2 Monthly Rate 3 Number of Months 10000 1% 28.91180402 Goal Seeking with Cell B5 found a solution Target value -400 Current value: (400.00) Pause OK Cancel Ans.:28.9 5 PMT (S400.00) Answer Ex2: Use FV function and Goal Seek. Planning for Your Retirement with Goal Seek In order to be able to live comfortably after retirement, you estimate that you will need 50,000 dollars each year for 20 years, starting one year from the date of retirement. In and after retirement is guaranteed by your pension company, what amount do you need to deposit each month? (Refer to Figure 3.4.7 for timing of payments.) Answers: EX2: (1). First calculate the future value of 360 payments, $ 800 each month at a 0.5% monthly rate. Use the Future Value function. The FV is $ 807,630.09. (2) Next use the mortgage payment function (PMT) to calculate the payment amount, using the future value in step (1) as the Present value. The monthly interest rate is 6%/12 (or 0.5%) and the number of payments equals 240. The calculated monthly payment (PMT) is $5,786.11 EX3: (make sure that B4 is a Future Value formula): Goal Seek -3000 10% OK Cancel B 1 Annual Deposit Set cel: $B$4 2 Number of Years: 30 To yalue: 1000000 3 Annual Rate By changing cel: $B$2 4 FV $542,830.27 5 Click the OK. The answer is 36.13 year. EX4: You have to use the Goal Seek function. In the following chart I randomly assumed that the monthly deposit before retirement is $300. My monthly payment received after retirement turned out to be $3,077.47. Use Goal Seek by setting cell D4 to value 5000. The monthly deposit will become $487.42. B D A 1 Monthly Deposit 300 PV =B4 closing, which is the beginning of the first period. Your first payment to the bank is at the end of the first period (type =0.) FY LO AN PV Future Value Function: Payments at the beginning of each period Present Value and PMT Function: Payments at end of each period ..... 1st Pd. 2nd Pd 60th Pd 2nd Pd 60th Pd 1st Pd. Fig. 3.3.8 Fig. 3.3.7. EXERCISE 2.3 2. You plan to deposit a fixed amount each year, at the beginning of the year, for ten years at a fixed 6 percent annual rate and you also wish to accumulate 500,000 dollars by the end of the tenth year, how much do you have to deposit in your pension fund each year? 3. The Dow Jones index grew in thirty years from 1870 on 9/1/1996 to 18454 on 9/1/2016. What is the average annual percent increase? Ex.2.3.2 Answer (1) Modify Fig. 2.3.3 as follows: Enter =A2 in B3, C4, D5, E6, 67, H8, 19 and J10. (2) Change the number 10000 in A2 to 20000, 25000, 40000 or any other reasonable amount until the value in K12 becomes 500000. Ans.: 35786.77 A 1 year 1 2 10000 3 4 5 6 7 8 9 10 11 12 B D E F G H 1 K Iyear 2 year 3 Iyear 4 Iyear 5 year 6 year 7 Iyear 8 year 9 year 10 Iyear 11 FA2*1.06 =B2*1.06 =C2"1.06 D2"1.06 E2*1.06 F2"1.06 G2 1.06 H2*1.06 12"1.06 J21.06 EAZ =B3"1.06 EC3 1.06 =D3"1.06 FE3"1.06 =F31.06 =G3 1.06 FH3"1.06 =13"1.06 J3"1.06 FAZ =C4*1.06 =24*1.06 E4*1.06 EF4*1.06 =G4*1.06 = 4*1.06 =141.06 34*1.06 AZ FD5 1.06 =E5*1.06 =F5 1.06 =G5 1.06 =15*1.06 =15 1.06 51.06 EA2 FE6 1.06 =F6"1.06 FG6 1.06 =H6 1.06 F16"1.06 FJ6 1.06 A2 =F7"1.06 EG7*1.06 =H71.06 17"1.06 J7"1.06 EA2 1=G891.06 =H8*1.06 =1891.06 128 1.06 EA2 H9 1.06 1991.06 239 1.06 FAZ F110 1.06 JIO 1.06 EAZ RJII 1.06 ESUM(K2:KIIT Note: This question can also be solved by the Future Value function and the Goal Seek procedure to be discussed in the next chapter. Figure 3.4.7 EXERCISE 3.4 continued 3. Ms. Melody decided to invest 800 dollars per month in her pension fund at the beginning of each month (6% annual rate), for thirty years, before her retirement. Ms. Melody also decided that, at time of retirement, she will not take out all of the accumulated money at once. Instead, she will take her money out in 240 equal monthly installments, beginning one month after the date of retirement ( refer to Figure 3.4.7 for timing of payments.) How much will Ms. Melody be receiving each month after retirement? 4. In section 3.4 (Fig. 3.4.2) our goal has been to accumulate 1,000,000 dollars by changing your annual investment amount. An alternative way to accumulate 1,000,000 dollars is to change the number of years of investment. At a 10% fixed annual rate, and at an annual investment of 3,000 dollars, how many years will be needed to reach the goal? 5. Suppose that you wish to receive 5,000 dollars, once a month, for 20 years after retirement. You also plan to invest once a month into your pension fund for 35 year before retirement. Your investment will start 35 years before the date of retirement, and will end one month before the date of retirement. The date of first payment to you will be one month after the date of retirement. Assuming that a fixed annual rate of 6% before 42 and after retirement is guaranteed by your pension company, what amount do you need to deposit each month? (Refer to Figure 3.4.7 for timing of payments.) Answers: EX2: (1). First calculate the future value of 360 payments, $ 800 each month at a 0.5% monthly rate. Use the Future Value function. The FV is $ 807,630.09. (2) Next use the mortgage payment function (PMT) to calculate the 33 Goal 1000000 OK Cancel Fig. 3.4.2 (formula version of Fig. 3.4.1) D $5,526,59 30 10% 28 Annual Deposit 29 year 30 Annual Return 31 32 FV 33 Goal Fig. 3.4.3 $1,000,000.00 $1,000,000.00 EXERCISE 3.4 1. Mr. Kenneth borrowed 10,000 dollars at the beginning of last month. The monthly rate is 1%, and is charged at end of each month. Mr. Kenneth wishes to pay off his debt by paying $400 dollars each month, starting beginning of this month. How long will it take in order to pay off the entire debt? (Refer to Figure3.3.8 for timing of payments.) 40 2. Use Goal Seek to redo Exercise 2.3.2. Answer Exl.: Use PMT function and use Goal Seek. Set B5 to -400 by changing B3. Goal Seek Status ? X Booki 1 Loan 2 Monthly Rate 3 Number of Months 10000 1% 28.91180402 Goal Seeking with Cell B5 found a solution Target value -400 Current value: (400.00) Pause OK Cancel Ans.:28.9 5 PMT (S400.00) Answer Ex2: Use FV function and Goal Seek. Planning for Your Retirement with Goal Seek In order to be able to live comfortably after retirement, you estimate that you will need 50,000 dollars each year for 20 years, starting one year from the date of retirement. In and after retirement is guaranteed by your pension company, what amount do you need to deposit each month? (Refer to Figure 3.4.7 for timing of payments.) Answers: EX2: (1). First calculate the future value of 360 payments, $ 800 each month at a 0.5% monthly rate. Use the Future Value function. The FV is $ 807,630.09. (2) Next use the mortgage payment function (PMT) to calculate the payment amount, using the future value in step (1) as the Present value. The monthly interest rate is 6%/12 (or 0.5%) and the number of payments equals 240. The calculated monthly payment (PMT) is $5,786.11 EX3: (make sure that B4 is a Future Value formula): Goal Seek -3000 10% OK Cancel B 1 Annual Deposit Set cel: $B$4 2 Number of Years: 30 To yalue: 1000000 3 Annual Rate By changing cel: $B$2 4 FV $542,830.27 5 Click the OK. The answer is 36.13 year. EX4: You have to use the Goal Seek function. In the following chart I randomly assumed that the monthly deposit before retirement is $300. My monthly payment received after retirement turned out to be $3,077.47. Use Goal Seek by setting cell D4 to value 5000. The monthly deposit will become $487.42. B D A 1 Monthly Deposit 300 PV =B4 closing, which is the beginning of the first period. Your first payment to the bank is at the end of the first period (type =0.) FY LO AN PV Future Value Function: Payments at the beginning of each period Present Value and PMT Function: Payments at end of each period ..... 1st Pd. 2nd Pd 60th Pd 2nd Pd 60th Pd 1st Pd. Fig. 3.3.8 Fig. 3.3.7. EXERCISE 2.3 2. You plan to deposit a fixed amount each year, at the beginning of the year, for ten years at a fixed 6 percent annual rate and you also wish to accumulate 500,000 dollars by the end of the tenth year, how much do you have to deposit in your pension fund each year? 3. The Dow Jones index grew in thirty years from 1870 on 9/1/1996 to 18454 on 9/1/2016. What is the average annual percent increase? Ex.2.3.2 Answer (1) Modify Fig. 2.3.3 as follows: Enter =A2 in B3, C4, D5, E6, 67, H8, 19 and J10. (2) Change the number 10000 in A2 to 20000, 25000, 40000 or any other reasonable amount until the value in K12 becomes 500000. Ans.: 35786.77 A 1 year 1 2 10000 3 4 5 6 7 8 9 10 11 12 B D E F G H 1 K Iyear 2 year 3 Iyear 4 Iyear 5 year 6 year 7 Iyear 8 year 9 year 10 Iyear 11 FA2*1.06 =B2*1.06 =C2"1.06 D2"1.06 E2*1.06 F2"1.06 G2 1.06 H2*1.06 12"1.06 J21.06 EAZ =B3"1.06 EC3 1.06 =D3"1.06 FE3"1.06 =F31.06 =G3 1.06 FH3"1.06 =13"1.06 J3"1.06 FAZ =C4*1.06 =24*1.06 E4*1.06 EF4*1.06 =G4*1.06 = 4*1.06 =141.06 34*1.06 AZ FD5 1.06 =E5*1.06 =F5 1.06 =G5 1.06 =15*1.06 =15 1.06 51.06 EA2 FE6 1.06 =F6"1.06 FG6 1.06 =H6 1.06 F16"1.06 FJ6 1.06 A2 =F7"1.06 EG7*1.06 =H71.06 17"1.06 J7"1.06 EA2 1=G891.06 =H8*1.06 =1891.06 128 1.06 EA2 H9 1.06 1991.06 239 1.06 FAZ F110 1.06 JIO 1.06 EAZ RJII 1.06 ESUM(K2:KIIT Note: This question can also be solved by the Future Value function and the Goal Seek procedure to be discussed in the next chapter. Figure 3.4.7 EXERCISE 3.4 continued 3. Ms. Melody decided to invest 800 dollars per month in her pension fund at the beginning of each month (6% annual rate), for thirty years, before her retirement. Ms. Melody also decided that, at time of retirement, she will not take out all of the accumulated money at once. Instead, she will take her money out in 240 equal monthly installments, beginning one month after the date of retirement ( refer to Figure 3.4.7 for timing of payments.) How much will Ms. Melody be receiving each month after retirement? 4. In section 3.4 (Fig. 3.4.2) our goal has been to accumulate 1,000,000 dollars by changing your annual investment amount. An alternative way to accumulate 1,000,000 dollars is to change the number of years of investment. At a 10% fixed annual rate, and at an annual investment of 3,000 dollars, how many years will be needed to reach the goal? 5. Suppose that you wish to receive 5,000 dollars, once a month, for 20 years after retirement. You also plan to invest once a month into your pension fund for 35 year before retirement. Your investment will start 35 years before the date of retirement, and will end one month before the date of retirement. The date of first payment to you will be one month after the date of retirement. Assuming that a fixed annual rate of 6% before 42 and after retirement is guaranteed by your pension company, what amount do you need to deposit each month? (Refer to Figure 3.4.7 for timing of payments.) Answers: EX2: (1). First calculate the future value of 360 payments, $ 800 each month at a 0.5% monthly rate. Use the Future Value function. The FV is $ 807,630.09. (2) Next use the mortgage payment function (PMT) to calculate the