Here we apply Bayesian inference to an everyday problem. Suppose we have a coin and are not sure if it is a fair coin or a double-headed coin. The two hypotheses would be Hf : p(H) = 0.5 and Hd : p(H) = 1. Our priors would be p(Hf ) = 0.999, p(Hd) = 0.001 and our data would be 6 successive heads.?Please Use R code!!!!Not mathematical method?

? Apply Bayes's theorem to calculate the posterior probabilities for Hf and Hd.

? With these priors, how many heads would you need to observe to take your posterior probability for Hd to exceed 0.5?

? (harder) Compare the results with a conventional frequentist analysis.

? Give an example of Bayes's theorem in your everyday life. State 2 or 3 hypotheses clearly, state your priors clearly, state your data clearly, state your likelihoods clearly and apply Bayes's theorem to your situation. Comment briefly on whether Bayesian logic is operating as expected in this situation.

?R code and explanation Please!! ?

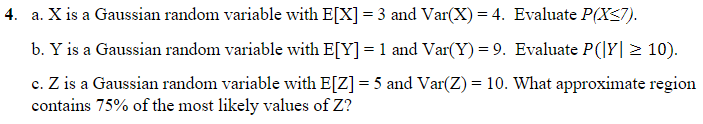
Consider the jointly Gaussian random variables X and Y that have the following joint PDF: H 2pxy f xx (x, y) = exp -+ 2TOXOY V1 - p2 2(1 - p2) 2 OXOY (a) Prove that Y is a Gaussian random variable by deriving its marginal PDF, fy (y). Find the mean and variance of Y. (b) Prove that fxy(xy) corresponds to another Gaussian random variable, then find its mean and variance.m 2 Let X be a Gaussian random variable independent of S with E[X] = 0 and P(S = 1) = P(S = -1) = 1/2. (i) Check that SX is a Gaussian random variable. (ii) Give an example of uncorrelated, zero-mean, Gaussian random variable X1 and X2 such that the vector X = (X1, X2) is not Gaussian, and where X1 and X2 are not independent.4. a. X is a Gaussian random variable with E[X] = 3 and Var(X) = 4. Evaluate P(X=7). b. Y is a Gaussian random variable with E[Y] = 1 and Var(Y) = 9. Evaluate P(|Y| = 10). c. Z is a Gaussian random variable with E[Z] = 5 and Var(Z) = 10. What approximate region contains 75% of the most likely values of Z?(EFCL) Find the moment generating function (MGF) for the following random variables. Use the MGF to compute the first and second moments and confirm that your answers are as expected. Hint: The integration technique known as completing the square of the exponent is necessary to complete these problems. I've discussed the technique below. a) A zero mean, unit variance Gaussian random variable, X ~ N(0,1) b) A zero mean Gaussian random variable with known variance, X - N(0,of ) c) A general Gaussian random variable, X - N(u,o')