Hey I do not really understand this assignment and I do not know how to go about this. can someone please help me I would appreciate this. thank you

I would prefer to focus on the linear programming model with sensetivity analysis.

take your time

Here are some extra infromation

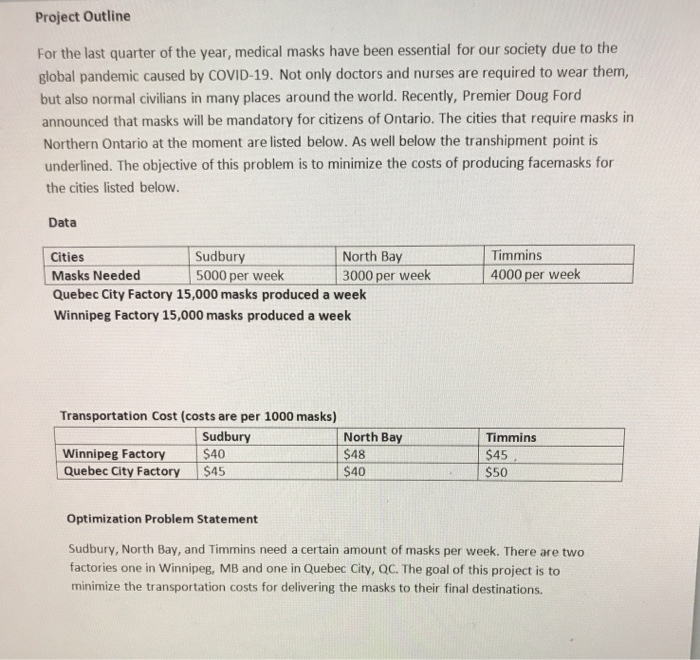
The take home exam provides you an opportunity to gain a deeper understanding of the optimum management of business resources (capital, labor, machines). You have to demonstrate your understanding by developing one of the following models of any business of your choice: 1. Linear programming model with sensitivity analysis 2. Integer programming model 3. Transportation, Assignment, or Transhipment model 4. Network model 5. Project scheduling (PERT/CPM) model You are free to choose any topic of your choice and demonstrate the application of one of the above optimization models in the business workplace. You will have to collect data for your project either from a real business or from any website. In particular you are required to do the following tasks: 1. Project outline (Due on Monday, July 13 at 4:00 pm): You should prepare and submit a brief project outline of the topic of your choice. The grading rubric for the project outline will be: a. Title (clear and concise) (2 marks) 1 b. Project outline (about 100 words) Why is the project important, and what data parameters (list all variables) have been collected either from a real business or from the website for optimization. (5 marks) c. Data: Submit your data along with all its source information (3 marks) d. Clear statement(s) of the optimization problem (5 marks) 2. Project Report and Optimization Model (Due on Monday, July 20 at 6:50 pm): Using your data, run the optimization model, and interpret the results obtained. You should clearly demonstrate your knowledge by writing all mathematical model equations for objective function and constraints. a. Mathematical equation for objective function and its description (5 marks) b. Mathematical equations for constraints and their description (5 marks) c. Project report: Write your report with the following headings: Objectives (about 50 words) (5 marks) Description of the model and its analysis (about 100 words) (7 marks) Description of results (about 100 words) (8 marks) Conclusions: Clearly state the implications of your results (about 50 words) (5 marks) Project Outline For the last quarter of the year, medical masks have been essential for our society due to the global pandemic caused by COVID-19. Not only doctors and nurses are required to wear them, but also normal civilians in many places around the world. Recently, Premier Doug Ford announced that masks will be mandatory for citizens of Ontario. The cities that require masks in Northern Ontario at the moment are listed below. As well below the transhipment point is underlined. The objective of this problem is to minimize the costs of producing facemasks for the cities listed below. Data Timmins 4000 per week Cities Sudbury North Bay Masks Needed 5000 per week 3000 per week Quebec City Factory 15,000 masks produced a week Winnipeg Factory 15,000 masks produced a week Transportation Cost (costs are per 1000 masks) Sudbury North Bay Winnipeg Factory $40 $48 Quebec City Factory $45 $40 mins $45 $50 Optimization Problem Statement Sudbury, North Bay, and Timmins need a certain amount of masks per week. There are two factories one in Winnipeg, MB and one in Quebec City, QC. The goal of this project is to minimize the transportation costs for delivering the masks to their final destinations. The take home exam provides you an opportunity to gain a deeper understanding of the optimum management of business resources (capital, labor, machines). You have to demonstrate your understanding by developing one of the following models of any business of your choice: 1. Linear programming model with sensitivity analysis 2. Integer programming model 3. Transportation, Assignment, or Transhipment model 4. Network model 5. Project scheduling (PERT/CPM) model You are free to choose any topic of your choice and demonstrate the application of one of the above optimization models in the business workplace. You will have to collect data for your project either from a real business or from any website. In particular you are required to do the following tasks: 1. Project outline (Due on Monday, July 13 at 4:00 pm): You should prepare and submit a brief project outline of the topic of your choice. The grading rubric for the project outline will be: a. Title (clear and concise) (2 marks) 1 b. Project outline (about 100 words) Why is the project important, and what data parameters (list all variables) have been collected either from a real business or from the website for optimization. (5 marks) c. Data: Submit your data along with all its source information (3 marks) d. Clear statement(s) of the optimization problem (5 marks) 2. Project Report and Optimization Model (Due on Monday, July 20 at 6:50 pm): Using your data, run the optimization model, and interpret the results obtained. You should clearly demonstrate your knowledge by writing all mathematical model equations for objective function and constraints. a. Mathematical equation for objective function and its description (5 marks) b. Mathematical equations for constraints and their description (5 marks) c. Project report: Write your report with the following headings: Objectives (about 50 words) (5 marks) Description of the model and its analysis (about 100 words) (7 marks) Description of results (about 100 words) (8 marks) Conclusions: Clearly state the implications of your results (about 50 words) (5 marks) Project Outline For the last quarter of the year, medical masks have been essential for our society due to the global pandemic caused by COVID-19. Not only doctors and nurses are required to wear them, but also normal civilians in many places around the world. Recently, Premier Doug Ford announced that masks will be mandatory for citizens of Ontario. The cities that require masks in Northern Ontario at the moment are listed below. As well below the transhipment point is underlined. The objective of this problem is to minimize the costs of producing facemasks for the cities listed below. Data Timmins 4000 per week Cities Sudbury North Bay Masks Needed 5000 per week 3000 per week Quebec City Factory 15,000 masks produced a week Winnipeg Factory 15,000 masks produced a week Transportation Cost (costs are per 1000 masks) Sudbury North Bay Winnipeg Factory $40 $48 Quebec City Factory $45 $40 mins $45 $50 Optimization Problem Statement Sudbury, North Bay, and Timmins need a certain amount of masks per week. There are two factories one in Winnipeg, MB and one in Quebec City, QC. The goal of this project is to minimize the transportation costs for delivering the masks to their final destinations