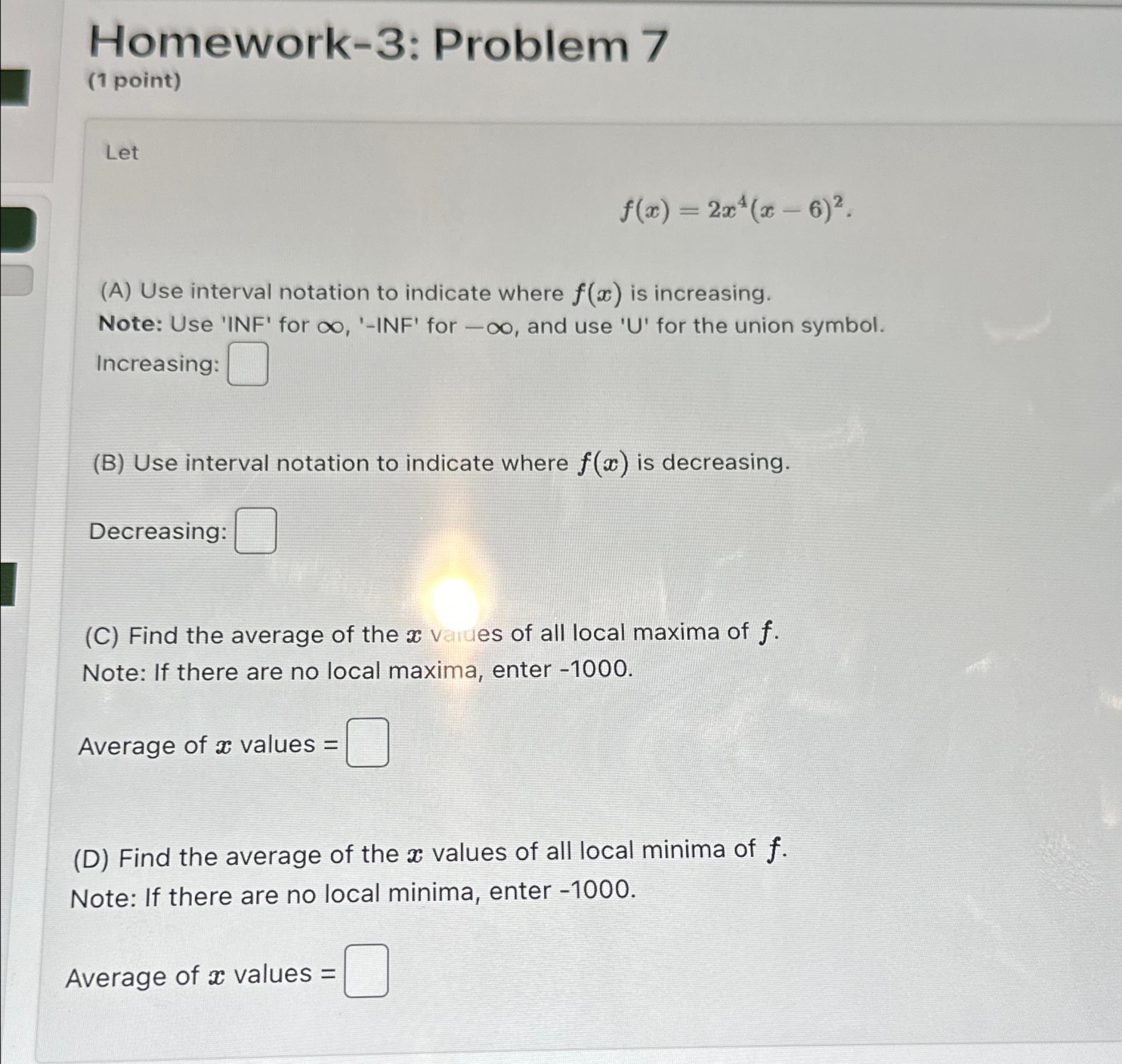
Question: Homework-3: Problem 7 (1 point) Let f(x)=2x^(4)(x-6)^(2) (A) Use interval notation to indicate where f(x) is increasing. Note: Use 'INF' for infty , '-INF'
Homework-3: Problem 7\ (1 point)\ Let\
f(x)=2x^(4)(x-6)^(2)\ (A) Use interval notation to indicate where
f(x)is increasing.\ Note: Use 'INF' for
\\\\infty , '-INF' for
-\\\\infty , and use '
U' for the union symbol.\ Increasing:\ (B) Use interval notation to indicate where
f(x)is decreasing.\ Decreasing:\ (C) Find the average of the
xvaues of all local maxima of
f.\ Note: If there are no local maxima, enter -1000.\ Average of
xvalues
=\ (D) Find the average of the
xvalues of all local minima of
f.\ Note: If there are no local minima, enter -1000.\ Average of
xvalues
= 
f(x)=2x4(x6)2. (A) Use interval notation to indicate where f(x) is increasing. Note: Use 'INF' for , '-INF' for , and use 'U' for the union symbol. Increasing: (B) Use interval notation to indicate where f(x) is decreasing. Decreasing: (C) Find the average of the x varues of all local maxima of f. Note: If there are no local maxima, enter -1000 . Average of x values = (D) Find the average of the x values of all local minima of f. Note: If there are no local minima, enter -1000
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


