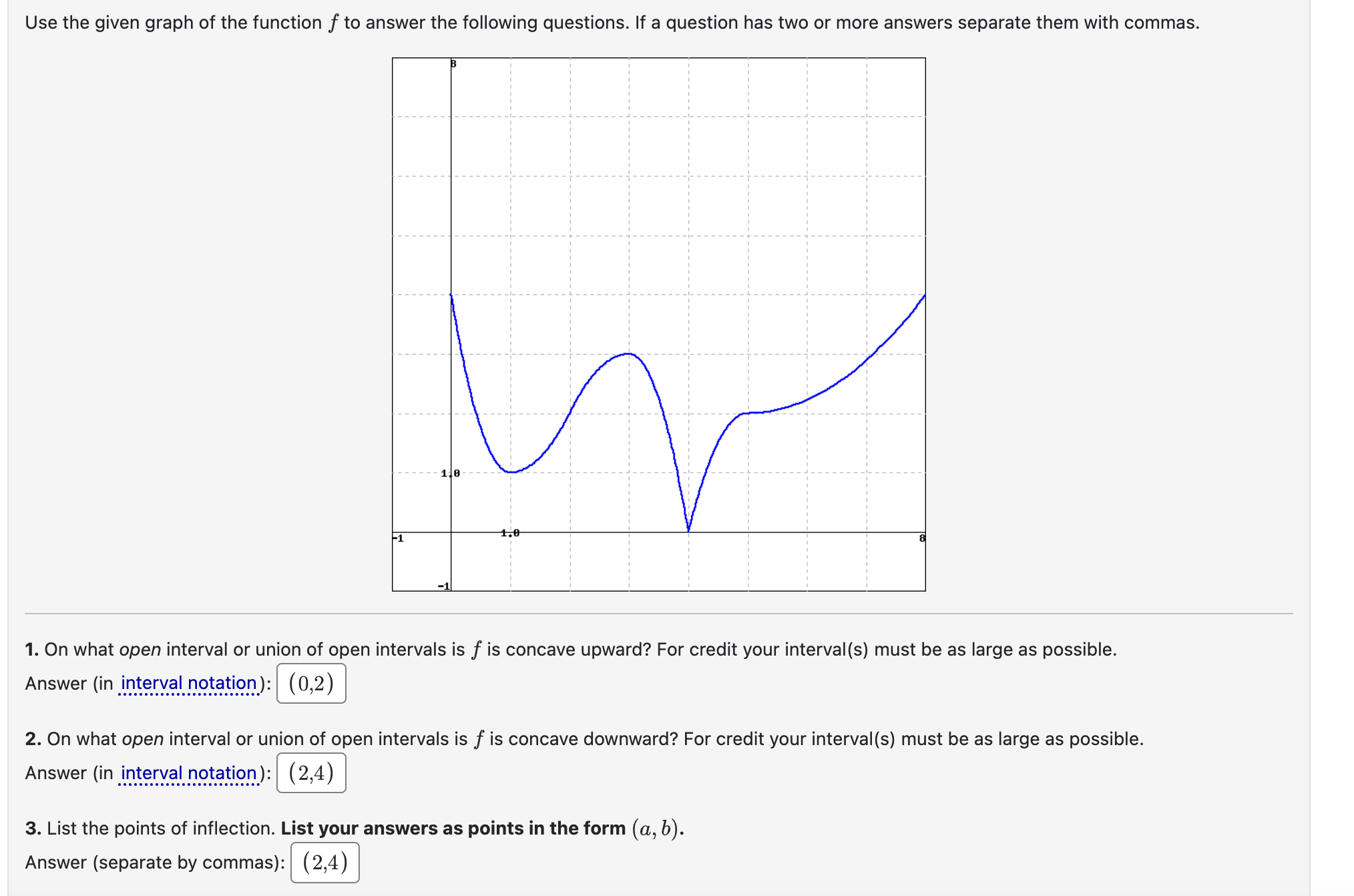
Let flz) = 2(z 8)* + 2. (A) Find all critical values and list them below. Note: If there are no critical values, enter 'NONE". (B) Use interval notation to indicate where f(m) is increasing. Note: Use 'INF' for oo, '-INF' for o0, and use 'U' for the union symbol. Increasing: [j (C) Use interval notation to indicate where f(z) is decreasing. Decreasing: E] (D) List the values of all local maxima of f. If there are no local maxima, enter 'NONE". z values of local maximums = [j (E) List the x values of all local minima of f. If there are no local minima, enter 'NONE". 2 values of local minimums = O f(z) = 2sin(z) cos(z) on (m, ) a) Find the critical numbers of f.| % 3747[ , % , J%Tn (Separate multiple answers by commas.) b) Determine the intervals on which f is increasing and decreasing. f is increasing on: f is decreasing on: Use the given graph of the function f to answer the following questions. If a question has two or more answers separate them with commas. B =1 1. On what open interval or union of open intervals is f is concave upward? For credit your interval(s) must be as large as possible. Answer (in interval notation):| (0,2) 2. On what open interval or union of open intervals is f is concave downward? For credit your interval(s) must be as large as possible. Answer (in interval notation): | (2,4) 3. List the points of inflection. List your answers as points in the form (a7 b). Answer (separate by commas): (2,4) a) Determine the intervals on which f is concave up and concave down. is concave up on: D f is concave down on: E] b) Based on your answer to part (a), determine the inflection points of f. Each point should be entered as an ordered pair (that is, in the form (z, y)). D (Separate multiple answers by commas.) c) Find the critical numbers of f and use the Second Derivative Test, when possible, to determine the relative extrema. List only the z-coordinates. Relative maxima at: (Separate multiple answers by commas.) Relative minima at: (Separate multiple answers by commas.) d) Find the z-value(s) where f'(z) has a relative maximum or minimum. f! has relative maxima at: (Separate multiple answers by commas.) has relative minima at: (Separate multiple answers by commas.)