how do i fix this problem

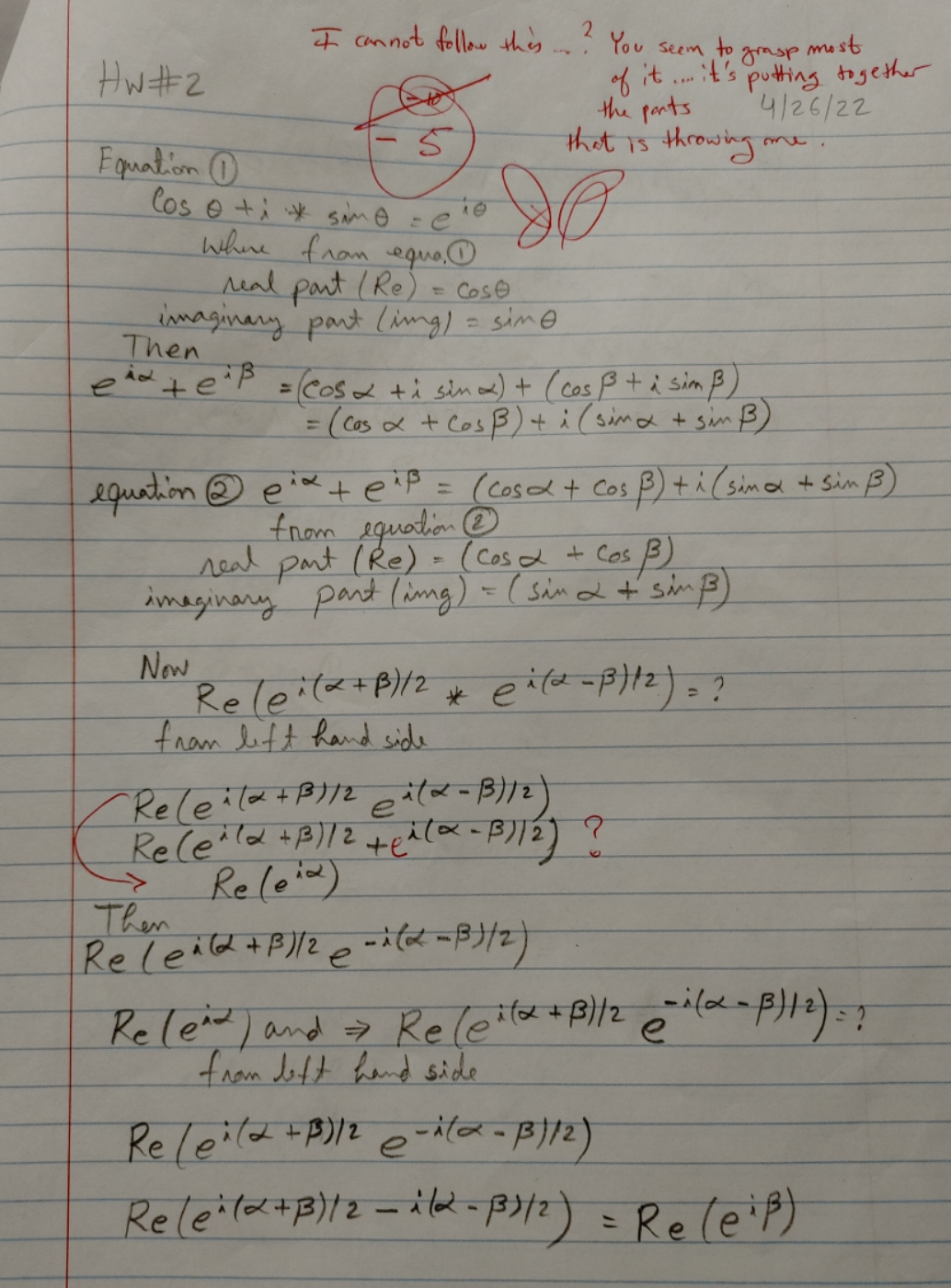
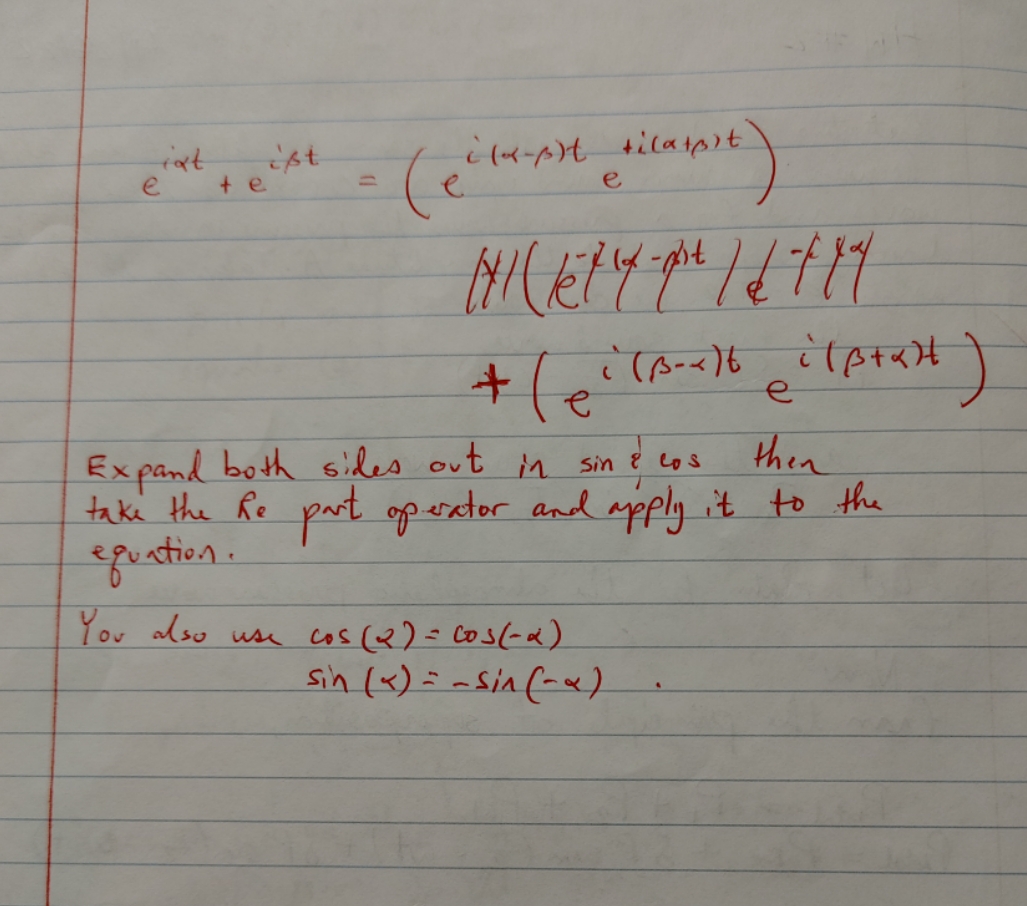
Problems Chapter 17 of "Physics for Scientists and Engineers", 10th ed. by Serway and Jewett. Two sound waves arrive at your car simultaneously; they have slightly different frequencies: wj and w2 and equal amplitudes. You hear the loudness oscillate sinusoidally; this is what we refer to as "beats". Show that the total sound wave has the the form: P(t) = Patm + 26P cos( (w1 - w2) /2) cos( (w1 + w2) /2). (1) You can use the trig identity in the text on p#.470 as a guide, but take the time to derive the iden- tity using de Moivre's theorem to apply the trick we've been developing in class for trig identities.I cannot follow this .. You seem to grasp most e HW # 2 of it . it's putting together the pants 4/26/ 22 Equation 5 that is throwing me Cos o + : $ simo reis Isthere from equal real part ( Re ) = cost Expand both sides out in sine cos then imaginary part ( ing ) = sime Then take the fe part operator and apply it to the eid tell = ( cost + i simm ) + ( cos p + i simp ) equation . = ( cos ox + Cos B ) + i ( simon + simp) You also use cos ( 2) = cos ( - * ) equation @ ex te'p = ( cosox + cos B ) + i ( simex + Sim B ) sin ( * ) = - sin ( - x ) from equation neal part ( Re ) " ( Cosex + Cos B ) imaginary part ( ing ) = ( sim ed + sim ] ) Now from left hand side Re( ella + B/2 gata - B)Z ) Re(ella + B ) / 2 + galax - B / / 2 ) ? Re(eid ) Them Re (ella + B ) / 2 0 - 1( = B)/2 ) Physics for Scientists and Engineers", 10th ed. by Serway and es arrive at your ear simultaneously; they have slightly different mplitudes. You hear the loudness oscillate sinusoidally; this is that the total sound wave has the the form: P (t) = Patm + 28P cos( ( w1 - W2) / 2) cos( (W1 + w2) / 2). trig identity in the text on p#.470 as a guide, but take the tim oivre's theorem to apply the trick we've been developing in claI can not follow this ? You seem to grasp most HW# 2 of it ... it's putting together the pants 4 / 26/ 22 Equation (1 5 that is throwing me. Cos o ti * simo = 210 where from eque. " real part ( Re ) = cose imaginary part ( ing ) = simo Then plate'P = (cost i simax ) + ( cos B + i simB) = ( cos ox + cos B ) + i ( simon + sim B ) equation 2 eid + e's = ( cosex+ cos B) ti ( simex + Sim B) from equation (2 ) real part ( Re ) = ( cost + Cos B ) imaginary part (ing ) = ( sin d + simp Now Re lei ( 2 + B ) 1 2 * ( x(2 - B/12 ) = ? from left hand side Re( ella + B/12 gila - B)/2 ) Re (eld + B / 12 + ph ( xx - 1) / 2 ) ? Re ( eid ) Then Re (ella + B)/ 2 0 - 1( 2 - B)/ 2 ) Re le's ) and = Re ( pita + B / / 2 - i(x - 1)12 ). from left hand side Re ( e :(2 + B)12 2 - itax - B) /2 ) Re (e " ( 2 + B ) 1 2 - 1 /2 - 13 )/2 ) = Releip )rat ist ((ex-p)t tilatpot e te e e Expand both sides out in sine cos then take the Re part operator and apply it to the equation . You also use cos ( 2) = cos ( - * ) sin ( 8 ) = - sin ( - * )