How do I write an RK4 (4th order Runge-Kutta) code in C which computes a system of three, first order, differential equations? I have started a code in C which computes a single first order differential equation I just need help converting that to solve this system:

S' = bSZ

Z' = bSZ + cR -aSZ

R' = dS + aSZ - cR

where a,b,c, and d are constants with values:

a = 0.005, b = 0.0095, c = 0.0001, d = 0.0001

The initial values of S, R, and Z are:

S(0) = 500

Z(0) = 0

R(0) = 0

The C code I have solves the differential equation:

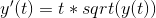
Here is the C code:

#include #include #include

double rk4(double(*f)(double, double), double h, double t, double y) { double dy1 = h * f(t, y), dy2 = h * f(t + h / 2, y + dy1 / 2), dy3 = h * f(t + h / 2, y + dy2 / 2), dy4 = h * f(t + h, y + dy3);

return y + (dy1 + 2 * dy2 + 2 * dy3 + dy4) / 6; }

double rate(double t, double y) { return t * sqrt(y); }

int main(void) { double *yout, t, y2; double t0 = 0, t1 = 10, h = .1; int i, n = 1 + (t1 - t0)/h; yout = malloc(sizeof(double) * n);

for (yout[0] = 1, i = 1; i

printf("x\tyout\trel. err. ------------ "); for (i = 0; i

return 0; }

y(t) = t * sqrt(y(t))