How do we go about this?

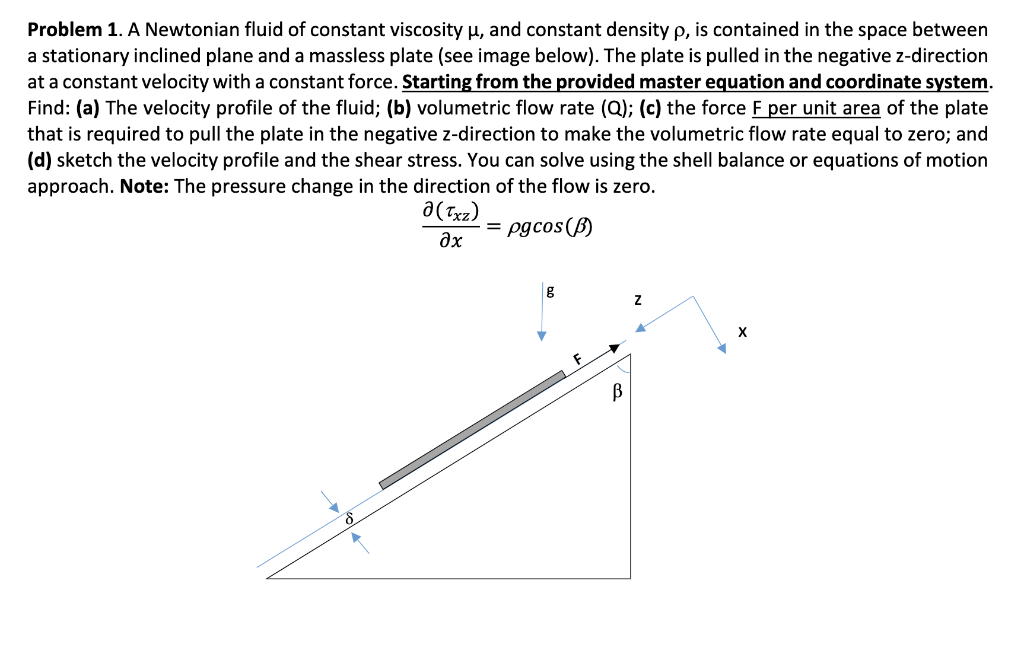
Problem 1. A Newtonian fluid of constant viscosity , and constant density , is contained in the space between a stationary inclined plane and a massless plate (see image below). The plate is pulled in the negative z-direction at a constant velocity with a constant force. Starting from the provided master equation and coordinate system. Find: (a) The velocity profile of the fluid; (b) volumetric flow rate (Q); (c) the force F per unit area of the plate that is required to pull the plate in the negative z-direction to make the volumetric flow rate equal to zero; and (d) sketch the velocity profile and the shear stress. You can solve using the shell balance or equations of motion approach. Note: The pressure change in the direction of the flow is zero. x(xz)=gcos() Problem 1. A Newtonian fluid of constant viscosity , and constant density , is contained in the space between a stationary inclined plane and a massless plate (see image below). The plate is pulled in the negative z-direction at a constant velocity with a constant force. Starting from the provided master equation and coordinate system. Find: (a) The velocity profile of the fluid; (b) volumetric flow rate (Q); (c) the force F per unit area of the plate that is required to pull the plate in the negative z-direction to make the volumetric flow rate equal to zero; and (d) sketch the velocity profile and the shear stress. You can solve using the shell balance or equations of motion approach. Note: The pressure change in the direction of the flow is zero. x(xz)=gcos()