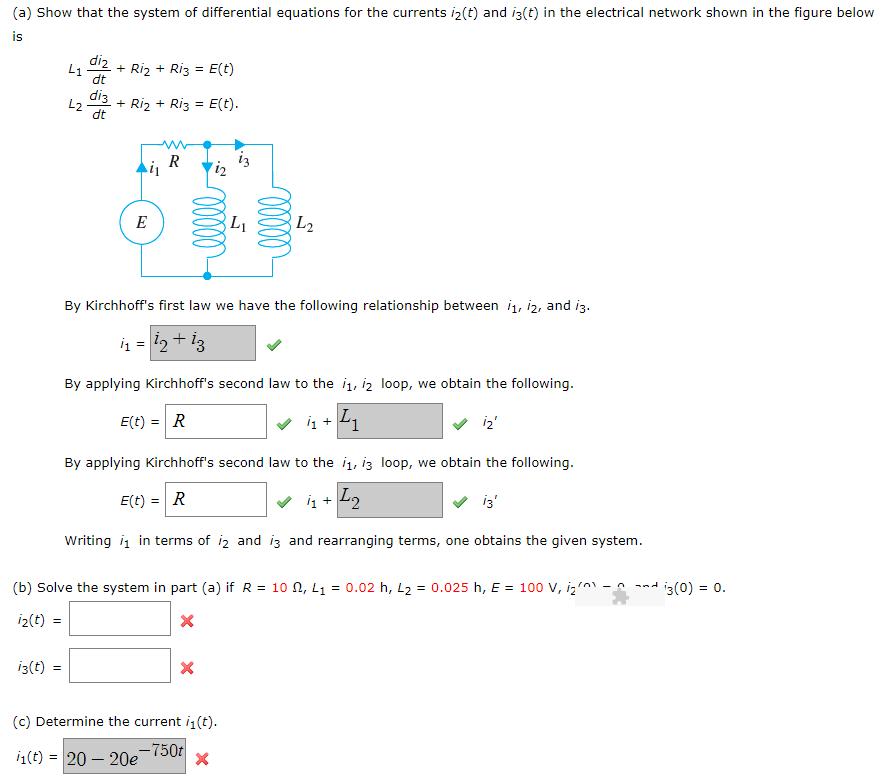
(a) Show that the system of differential equations for the currents iz(t) and iz(t) in the electrical network shown in the figure below is diz dt + Riz + Riz = E(t) L1 %3D diz + Riz + Riz = E(t). L2 dt %3! R iz E L1 L2 By Kirchhoff's first law we have the following relationship between i, i2, and iz. By applying Kirchhoff's second law to the i1, iz loop, we obtain the following. E(t) = R i + By applying Kirchhoff's second law to the i1, i3 loop, we obtain the following. E(t) = R ij + Writing i in terms of iz and iz and rearranging terms, one obtains the given system. (b) Solve the system in part (a) if R = 10 N, L1 = 0.02 h, L2 = 0.025 h, E = 100 V, iz' - --d ig(0) = 0. iz(t) i3(t) = (c) Determine the current i1(t). '1(t) = 20 20e-750t