I have this question where i am stuck on finding the particular solution, and i am having trouble understanding the professors solution, here is how much i was able to complete and following this in grey is the solution provided by professor, please help me understand what he is doing and why, thankyou

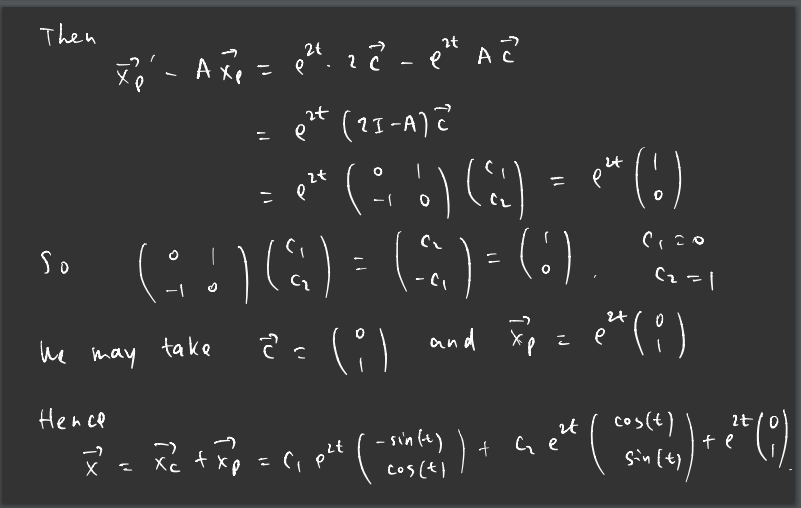
3 ) find general solution to system of ODE's x = ( 7 2 ) 2 + ( ) x ' = 2x, - 2 + 2+ x' = x, - 2x , (2 73 2 2 ) for A= 2+i (1- >) (2-)) +1 = 0 4 - 41 +12 + 1 = D -ia - b = 0 12- 41+42-1 a- ib = 0 (x- 2) (4-2 )=-1 - ai = b (x-2)2 =-1 * - 2 = V-T (i) 1= 2 + ; ed = p ( 2 +1 ) euler's formula: e= cosa + isink atz (2tilt - 2+ + it e 2t pit = ent foos ( + ) + ( i) sin ( + ) ( : ) . It cos ( + ) +isin ( ) ] = ie " [ cost + isint elt [ cost + isint ] = iest cost + ize 2+ sint catcost + ie ? *sint iest cost - eatsint e cost + ieltsint 2+ cost don't need = i(extant ) + (- ell sant i anymore ( cost - e2t ant 2t cost Xe = ci( extcost 2+\fProb 3 : Find the general solution to 2 X'= AX + ( A = Solution : The eigenvalues : det [ A - NI ] = (2-A) + 1 = 0. > = 2 +1, 12 = 2-1 The eigenvector Vi = ( an) of d1 = 2 + 1" - 191 -92 ( A - 7,I ) V = = So a, = ide and we take 92 =1 and 91= 1. Then Since ( 2 + ( ) t ( :) = ( cost + isint ) ( : ) ("cos(e ) . i - e" sin (t ) put cos( t ) + 1. " sim (E ) e" since ) C . p cos(E ) ( 2t cos ( * ) elt son(t) the complementary solution : cos( t ) X's = 6, put (- sinfty + cos ( * ) Sin [ t ) Guess the particular solution\f