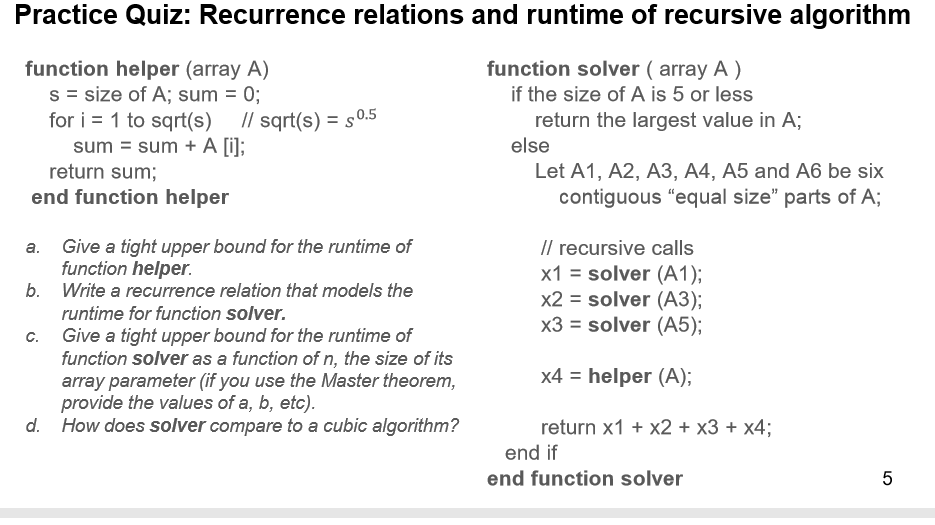
I know the answer is 3T(n/6)+squareroot(n)

and since a = 3

b = 6

and d= square root

then a>b = n(log^b*a)

however Im confused on how the six got their? and also if you could answer the questions so I can see where their coming from

like QA shouldn't that just be squarerootN

QB shouldn't that just be 3T(n/6)

QC

and since a = 3

b = 6

and d= square root

then a>b = n(log^b*a)

is that right?

Practice Quiz: Recurrence relations and runtime of recursive algorithm function helper (array A) function solver (array A) s- size of A; sum for i-1 to sqrt(s) 0; if the size of A is 5 or less sqrt(s)-s0.5 return the largest value in A; sum sum A [; else return sum; Let A1, A2, A3, A4, A5 and A6 be six end function helper a. Give a tight upper bound for the runtime of b. Write a recurrence relation that models the c. Give a tight upper bound for the runtime of contiguous "equal size" parts of A // recursive calls x1solver (A1); x2 solver (A3); x3solver (A5); function helper, runtime for function solver. function solver as a function of n, the size of its array parameter (if you use the Master theorem provide the values of a, b, eto) How does solver compare to a cubic algorithm? x4 helper (A); d. return x1 x2 x3 + x4 end if end function solver