Need help with this java code to print the same output shown below

public class PrintAdjacencyMatrix { public static void main(String[] args) { // adjacency matrix int [][] distance = {{-1,-1,18,16,-1,-1,-1,-1,-1,-1,-1,6,-1,-1,-1,-1,-1,-1,6,-1,-1,-1,5,-1}, //0 {-1,-1,-1,-1,22,-1,-1,-1,-1,-1,16,-1,16,-1,-1,-1,-1,-1,-1,5,13,-1,16,-1}, {18,-1,-1,7,5,7,-1,6,19,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,16,-1,-1}, {16,-1,7,-1,6,-1,-1,4,-1,15,-1,16,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,14,11}, {-1,22,5,6,-1,5,-1,-1,25,-1,-1,-1,-1,-1,-1,9,-1,-1,-1,-1,10,-1,11,-1}, {-1,-1,7,-1,5,-1,-1,-1,-1,-1,-1,-1,-1,7,-1,5,-1,-1,-1,-1,-1,-1,-1,-1}, {-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,16,5,18,-1,-1,-1}, {-1,-1,6,4,-1,-1,-1,-1,22,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,15,-1,11}, {-1,-1,19,-1,25,-1,-1,22,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,19,-1,-1},//8 {-1,-1,-1,15,-1,-1,-1,-1,-1,-1,-1,3,-1,-1,-1,-1,6,-1,-1,-1,-1,-1,-1,8},//9 {-1,16,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,2,-1,-1,-1,-1,-1,-1,-1,10,-1,-1,-1},//10 {6,-1,-1,16,-1,-1,-1,-1,-1,3,-1,-1,-1,-1,-1,-1,5,-1,-1,-1,-1,-1,-1,9},//11 {-1,16,-1,-1,-1,-1,-1,-1,-1,-1,2,-1,-1,-1,-1,5,-1,6,-1,-1,8,-1,-1,-1},//12 {-1,-1,-1,-1,-1,7,-1,-1,-1,-1,-1,-1,-1,-1,-1,6,-1,8,-1,-1,-1,-1,-1,-1},//13 {-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,8,-1,-1,-1,-1},//14 {-1,-1,-1,-1,9,5,-1,-1,-1,-1,-1,-1,5,6,-1,-1,-1,10,-1,-1,9,-1,10,-1},//15 {-1,-1,-1,-1,-1,-1,-1,-1,-1,6,-1,5,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,5},//16 {-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,6,8,-1,10,-1,-1,-1,-1,-1,-1,-1,-1},//17 {6,-1,-1,-1,-1,-1,16,-1,-1,-1,-1,-1,-1,-1,8,-1,-1,-1,-1,12,6,-1,8,-1},//18 {-1,5,-1,-1,-1,-1,5,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,12,-1,15,-1,-1,-1},//19 {-1,13,-1,-1,10,-1,18,-1,-1,-1,10,-1,8,-1,-1,9,-1,-1,6,15,-1,-1,6,-1},//20 {-1,-1,16,-1,-1,-1,-1,15,19,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1},//21 {5,16,-1,14,11,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,10,-1,-1,8,-1,6,-1,-1,-1},//22 {-1,-1,-1,11,-1,-1,-1,11,-1,8,-1,9,-1,-1,-1,-1,5,-1,-1,-1,-1,-1,-1,-1}}; //23 //Printing the header System.out.println("============================== "+ " ADJACENCY MATRIX OF SINGAPORE "+ "=============================="); // Printing the location index numbers for(int i=0;i

Dijkstra:

import java.util.ArrayList; import java.util.Collections; import java.util.List; import java.util.PriorityQueue;

public class Dijkstra { public void computePath(Vertex sourceVertex) { sourceVertex.setMinDistance(0); PriorityQueue priorityQueue = new PriorityQueue(); priorityQueue.add(sourceVertex);

while (!priorityQueue.isEmpty()) { Vertex vertex = priorityQueue.poll();

for (Edge edge : vertex.getEdges()) { Vertex v = edge.getTargetVertex(); double weight = edge.getWeight(); double minDistance = vertex.getMinDistance() + weight;

if (minDistance

public List getShortestPathTo(Vertex targetVerte) { List path = new ArrayList();

for (Vertex vertex = targetVerte; vertex != null; vertex = vertex.getPreviosVertex()) { path.add(vertex); }

Collections.reverse(path); return path; } }

App:

public class App { public static void main(String[] args) { Vertex v1 = new Vertex("A"); Vertex v2 = new Vertex("B"); Vertex v3 = new Vertex("C");

v1.Add_neighbour(new Edge(1, v1, v2)); v1.Add_neighbour(new Edge(10, v1, v2));

v2.Add_neighbour(new Edge(1, v2, v3));

Dijkstra dijkstra = new Dijkstra(); dijkstra.computePath(v1);

System.out.println(dijkstra.getShortestPathTo(v3)); } }

Edge:

public class Edge { private double weight; private Vertex startVertex; private Vertex targetVertex;

public Edge(double weight, Vertex startVertex, Vertex targetVertex) { this.weight = weight; this.startVertex = startVertex; this.targetVertex = targetVertex; }

public double getWeight() { return weight; } public Vertex getStartVertex() { return startVertex; }

public Vertex getTargetVertex() { return targetVertex; }

public void setWeight(double weight) { this.weight = weight; }

public void setStartVertex(Vertex startVertex) { this.startVertex = startVertex; }

public void setTargetVertex(Vertex targetVertex) { this.targetVertex = targetVertex; } }

Vertex:

import java.util.ArrayList; import java.util.List;

public class Vertex implements Comparable { private String name; private List edges; private boolean visited; private Vertex previosVertex; private double minDistance = Double.MAX_VALUE;

public Vertex(String name) { this.name = name; this.edges = new ArrayList(); }

public void Add_neighbour(Edge edge) { this.edges.add(edge); }

public List getEdges() { return edges; }

public void setEdges(List edges) { this.edges = edges; }

public boolean isVisited() { return visited; }

public void setVisited(boolean visited) { this.visited = visited; }

public void setPreviosVertex(Vertex previosVertex) { this.previosVertex = previosVertex; }

public void setMinDistance(double minDistance) { this.minDistance = minDistance; } public Vertex getPreviosVertex() { return previosVertex; }

public double getMinDistance() { return minDistance; }

@Override public String toString() { return name; }

@Override public int compareTo(Vertex otherVertex) { return Double.compare(this.minDistance, otherVertex.minDistance); } }

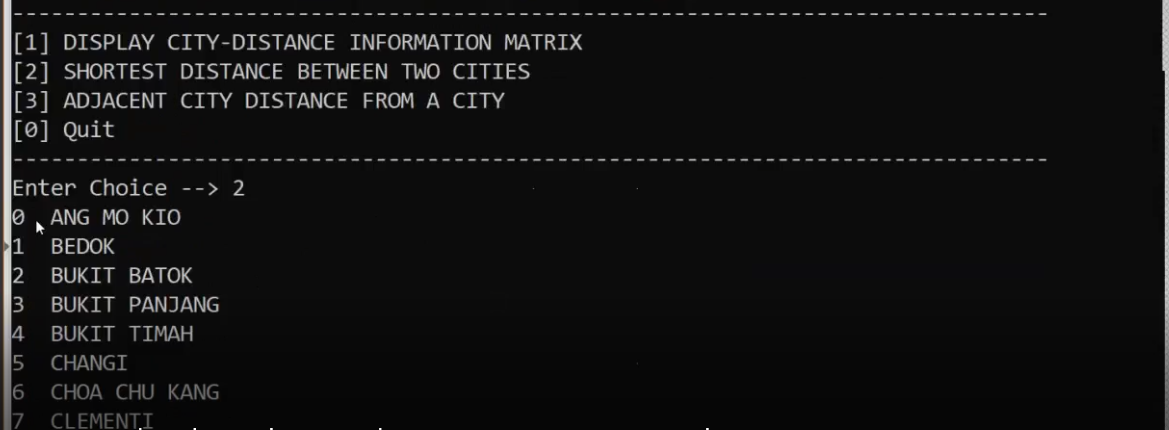
Java code output has to appear something like this, showing the start from, To, path, and total distance after entering the integer starting point and integer end point.

Here is the requirements needed for the question (need help with requirement 2,3, and 4)

Picture of adjacency matrix for viewing of distance (Do download to zoom)

[1] DISPLAY CITY-DISTANCE INFORMATION MATRIX [2] SHORTEST DISTANCE BETWEEN TWO CITIES [3] ADJACENT CITY DISTANCE FROM A CITY [0] Quit Enter Choice --> 2 0 ANG MO KIO 1 BEDOK 2 BUKIT BATOK 3 BUKIT PANJANG 4 BUKIT TIMAH 5 CHANGI 6 CHOA CHU KANG CLEMENTI 18 SERANGOON 19 TAMPINES 20 TOA PAYOH 21 TUAS 22 UPPER THOMSON 23 WOODLANDS Select a integer starting point: 0 Select a integer end point: 9 Start from: ANG MO KIO To: MANDAI Path: ANG MO KIO -> NEE SOON -> MANDAI Total Distance: 9km Requirement 1 - Representation of the map in Figure 1 Represent the city-distance information shown in the map in Figure 1 with a weighted graph using adjacency matrix or link-list. Sembawang Woodlands 5 6 19 9 GO 5 Choa Chu Kang 5/ 14 15 22 Bukit 6 18 Mandal 3 Punggol Nee Soon 11/15 16 6 Sakit 16 Ang Mo Kio 8 6 16 Changi Ranjang 7 6 18 8 Serangoon 12 5 ypper 6 11 Thomson 16 Tampines Batak 15 Bukit 16 19/ 22 Simah 5 10 10 Noa Payoh 16 9 Bedok 5 Clement 8l VO Marina Bay Queenstown 6 16 Pasir 5 Panjang Outram 10 8 16 Fuas 257 59 19 Jurong 5 OD Soniusa Figure 1 Requirement 2 - Implementation Write an interactive program that given the start and destination cities, will determine the shortest route between them and its total distance. It is all right to have 0 distance; i.e., start and end at the same city. You can assume that the roads are all bi-direction; i.e., vehicle can travel in both directions. The output of your program may look something similar as follow: Start from: Changi To: Choa Chu Kang Path: Changi -> Toa Payoh -> Bukit Timah -> Bukit Batok -> Choa Chu Kang Total distance: 39 Km. Requirement 3 - Test run Test your program by determining the following routes: Changi to Choa Chu Kang Bedok to Bukit Batok Marina Bay to Woodlands Sembawang to Bukit Timah Upper Thomson to Outram Bukit Batok to Tampines Requirement 4 - Program Complexity Derive the program running time complexity of your algorithm using Big-O notation. State clearly how you arrive at the Big-O notation. Partial marks will be awarded only for stating without showing the work in arriving at your conclusion. 21 2 Bukit Batok 18 3 Bukit Panjang 16 5 Clementi Bukit Timah Bedok 6 Changi Cho Chu Karig 8 Jurong 9 Mandai 12 Outram 11 Nee Soon 6 13 Pasir Panjang 10 Marina Bay . 16 14 Punggol 15 Queenstown 17 Sentosa 16 Sembawang 18 Serangoon 6 19 Tampines 20 Toa Payoh Tuas 22 23 Upper Thomson Woodlands 5 16 . = 16 = = = 5 13 7 22 5 6 7 19 Index 0 1 2 3 4 5 6 7 16 6 4 4 = 15 90 16 = = = 11 7. 5 7 6 5 se 22 19 25 10 9 5 14 11 = 5 7 16 5 18 - 4 = 22 = 6 19 11 15 19 25 22 . 15 2 3 = . 8 16 . 2 2 6 . 5 10 Index 0 To | From Ang Mo Kio Ang Mo Kio Bedok Bukit Batok 18 Bukit Panjang 16 Bukit Timah Clementi = Changi ChaChu Karig Jurong Mandai Marina Bay Nee Soon 6 6 Outram Pasir Panjang = Punggol Queenstown Sembawang Sentosa Serangoon 6 Tampines Toa Payoh Tuas = Upper Thomson 5 Woodlands = 16 = = 3 = = = -- . 9 16 2 8 8 5 6 = 6 8 7 = = = 8 = 9 9 5 19 5 6 = -- 10 9 9 = 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 10 6 5 . . 5 - = 6 8 10 e = . 8 8 12 = 16 5 18 = 6 15 19 = 5 13 = - 8 = 6 = 10 10 8 9 12 6 . 8 . = 15 16 15 19 = 16 11 10 6 14 11 11 8 9 5 = [1] DISPLAY CITY-DISTANCE INFORMATION MATRIX [2] SHORTEST DISTANCE BETWEEN TWO CITIES [3] ADJACENT CITY DISTANCE FROM A CITY [0] Quit Enter Choice --> 2 0 ANG MO KIO 1 BEDOK 2 BUKIT BATOK 3 BUKIT PANJANG 4 BUKIT TIMAH 5 CHANGI 6 CHOA CHU KANG CLEMENTI 18 SERANGOON 19 TAMPINES 20 TOA PAYOH 21 TUAS 22 UPPER THOMSON 23 WOODLANDS Select a integer starting point: 0 Select a integer end point: 9 Start from: ANG MO KIO To: MANDAI Path: ANG MO KIO -> NEE SOON -> MANDAI Total Distance: 9km Requirement 1 - Representation of the map in Figure 1 Represent the city-distance information shown in the map in Figure 1 with a weighted graph using adjacency matrix or link-list. Sembawang Woodlands 5 6 19 9 GO 5 Choa Chu Kang 5/ 14 15 22 Bukit 6 18 Mandal 3 Punggol Nee Soon 11/15 16 6 Sakit 16 Ang Mo Kio 8 6 16 Changi Ranjang 7 6 18 8 Serangoon 12 5 ypper 6 11 Thomson 16 Tampines Batak 15 Bukit 16 19/ 22 Simah 5 10 10 Noa Payoh 16 9 Bedok 5 Clement 8l VO Marina Bay Queenstown 6 16 Pasir 5 Panjang Outram 10 8 16 Fuas 257 59 19 Jurong 5 OD Soniusa Figure 1 Requirement 2 - Implementation Write an interactive program that given the start and destination cities, will determine the shortest route between them and its total distance. It is all right to have 0 distance; i.e., start and end at the same city. You can assume that the roads are all bi-direction; i.e., vehicle can travel in both directions. The output of your program may look something similar as follow: Start from: Changi To: Choa Chu Kang Path: Changi -> Toa Payoh -> Bukit Timah -> Bukit Batok -> Choa Chu Kang Total distance: 39 Km. Requirement 3 - Test run Test your program by determining the following routes: Changi to Choa Chu Kang Bedok to Bukit Batok Marina Bay to Woodlands Sembawang to Bukit Timah Upper Thomson to Outram Bukit Batok to Tampines Requirement 4 - Program Complexity Derive the program running time complexity of your algorithm using Big-O notation. State clearly how you arrive at the Big-O notation. Partial marks will be awarded only for stating without showing the work in arriving at your conclusion. 21 2 Bukit Batok 18 3 Bukit Panjang 16 5 Clementi Bukit Timah Bedok 6 Changi Cho Chu Karig 8 Jurong 9 Mandai 12 Outram 11 Nee Soon 6 13 Pasir Panjang 10 Marina Bay . 16 14 Punggol 15 Queenstown 17 Sentosa 16 Sembawang 18 Serangoon 6 19 Tampines 20 Toa Payoh Tuas 22 23 Upper Thomson Woodlands 5 16 . = 16 = = = 5 13 7 22 5 6 7 19 Index 0 1 2 3 4 5 6 7 16 6 4 4 = 15 90 16 = = = 11 7. 5 7 6 5 se 22 19 25 10 9 5 14 11 = 5 7 16 5 18 - 4 = 22 = 6 19 11 15 19 25 22 . 15 2 3 = . 8 16 . 2 2 6 . 5 10 Index 0 To | From Ang Mo Kio Ang Mo Kio Bedok Bukit Batok 18 Bukit Panjang 16 Bukit Timah Clementi = Changi ChaChu Karig Jurong Mandai Marina Bay Nee Soon 6 6 Outram Pasir Panjang = Punggol Queenstown Sembawang Sentosa Serangoon 6 Tampines Toa Payoh Tuas = Upper Thomson 5 Woodlands = 16 = = 3 = = = -- . 9 16 2 8 8 5 6 = 6 8 7 = = = 8 = 9 9 5 19 5 6 = -- 10 9 9 = 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 10 6 5 . . 5 - = 6 8 10 e = . 8 8 12 = 16 5 18 = 6 15 19 = 5 13 = - 8 = 6 = 10 10 8 9 12 6 . 8 . = 15 16 15 19 = 16 11 10 6 14 11 11 8 9 5 =