I need all the possible process

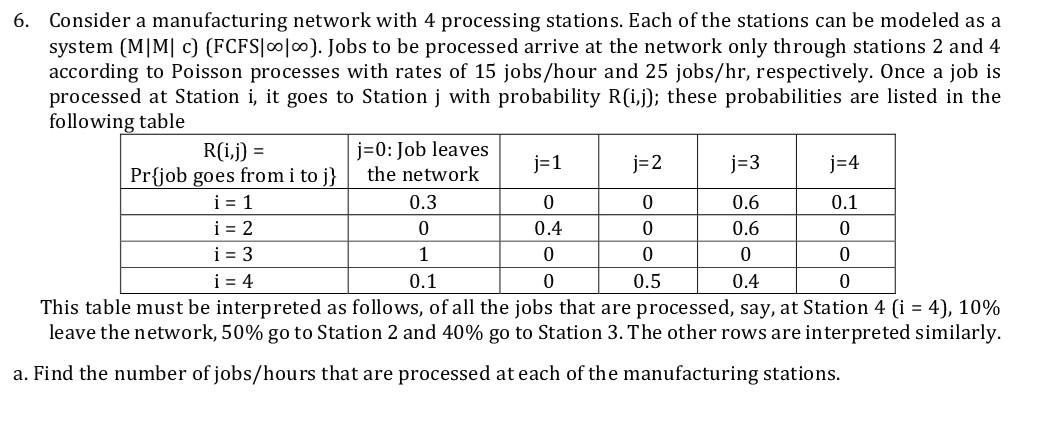
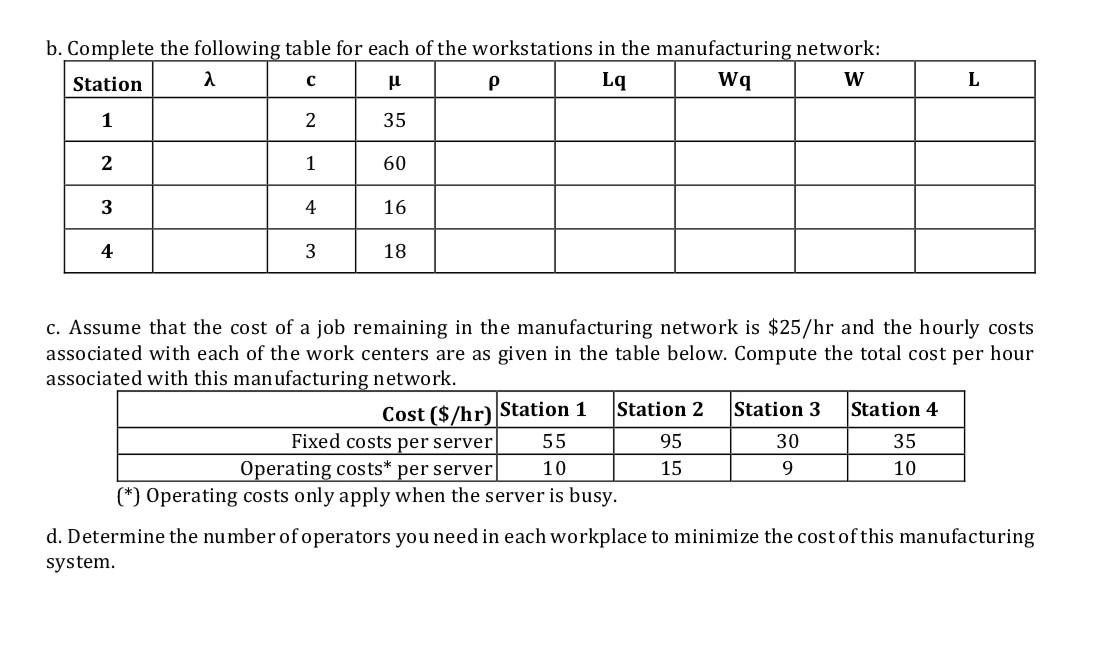
6. Consider a manufacturing network with 4 processing stations. Each of the stations can be modeled as a system (MMC) (FCFS|00|00). Jobs to be processed arrive at the network only through stations 2 and 4 according to Poisson processes with rates of 15 jobs/hour and 25 jobs/hr, respectively. Once a job is processed at Station i, it goes to Station j with probability R[i,j]; these probabilities are listed in the following table R(i,j) = j=0: Job leaves j=1 j=2 j=3 the network j=4 Pr{job goes from i to j} i = 1 0.3 0 0.6 0.1 i = 2 0.4 0.6 i = 3 1 0 0 0 i = 4 0.1 0.5 0.4 0 This table must be interpreted as follows, of all the jobs that are processed, say, at Station 4 (i = 4), 10% leave the network, 50% go to Station 2 and 40% go to Station 3. The other rows are interpreted similarly. a. Find the number of jobs/hours that are processed at each of the manufacturing stations. 0 0 0 0 0 b. Complete the following table for each of the workstations in the manufacturing network: Station u Lq Wq W L 1 2 35 2 1 60 3 4 16 4 3 18 c. Assume that the cost of a job remaining in the manufacturing network is $25/hr and the hourly costs associated with each of the work centers are as given in the table below. Compute the total cost per hour associated with this manufacturing network. Cost ($/hr) Station 1 Station 2 Station 3 Station 4 Fixed costs per server 55 95 30 35 Operating costs* per server 10 15 9 10 *) Operating costs only apply when the server is busy. d. Determine the number of operators you need in each workplace to minimize the cost of this manufacturing system. 6. Consider a manufacturing network with 4 processing stations. Each of the stations can be modeled as a system (MMC) (FCFS|00|00). Jobs to be processed arrive at the network only through stations 2 and 4 according to Poisson processes with rates of 15 jobs/hour and 25 jobs/hr, respectively. Once a job is processed at Station i, it goes to Station j with probability R[i,j]; these probabilities are listed in the following table R(i,j) = j=0: Job leaves j=1 j=2 j=3 the network j=4 Pr{job goes from i to j} i = 1 0.3 0 0.6 0.1 i = 2 0.4 0.6 i = 3 1 0 0 0 i = 4 0.1 0.5 0.4 0 This table must be interpreted as follows, of all the jobs that are processed, say, at Station 4 (i = 4), 10% leave the network, 50% go to Station 2 and 40% go to Station 3. The other rows are interpreted similarly. a. Find the number of jobs/hours that are processed at each of the manufacturing stations. 0 0 0 0 0 b. Complete the following table for each of the workstations in the manufacturing network: Station u Lq Wq W L 1 2 35 2 1 60 3 4 16 4 3 18 c. Assume that the cost of a job remaining in the manufacturing network is $25/hr and the hourly costs associated with each of the work centers are as given in the table below. Compute the total cost per hour associated with this manufacturing network. Cost ($/hr) Station 1 Station 2 Station 3 Station 4 Fixed costs per server 55 95 30 35 Operating costs* per server 10 15 9 10 *) Operating costs only apply when the server is busy. d. Determine the number of operators you need in each workplace to minimize the cost of this manufacturing system