I NEED HELP ASAP (USING EXCEL)

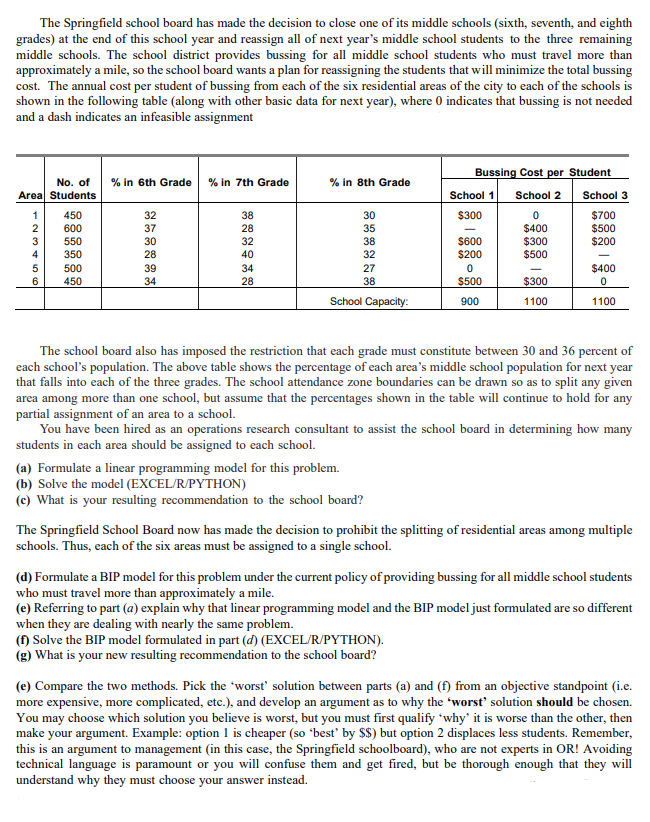
The Springfield school board has made the decision to close one of its middle schools (sixth, seventh, and eighth grades) at the end of this school year and reassign all of next year's middle school students to the three remaining middle schools. The school district provides bussing for all middle school students who must travel more than approximately a mile, so the school board wants a plan for reassigning the students that will minimize the total bussing cost. The annual cost per student of bussing from each of the six residential areas of the city to each of the schools is shown in the following table (along with other basic data for next year), where 0 indicates that bussing is not needed and a dash indicates an infeasible assignment % in 6th Grade % in 7th Grade % in 8th Grade No. of Area Students 1 450 2 600 3 550 4 350 5 500 6 450 32 37 30 28 39 34 38 28 32 40 34 28 30 35 38 32 27 38 Bussing Cost per Student School 1 School 2 School 3 $300 0 $700 $400 $500 $600 $300 $200 $200 $500 0 $400 $500 $300 0 900 1100 1100 School Capacity: The school board also has imposed the restriction that each grade must constitute between 30 and 36 percent of each school's population. The above table shows the percentage of each area's middle school population for next year that falls into each of the three grades. The school attendance zone boundaries can be drawn so as to split any given area among more than one school, but assume that the percentages shown in the table will continue to hold for any partial assignment of an area to a school. You have been hired as an operations research consultant to assist the school board in determining how many students in each area should be assigned to each school. (a) Formulate a linear programming model for this problem. (b) Solve the model (EXCEL/R/PYTHON) @) What is your resulting recommendation to the school board? The Springfield School Board now has made the decision to prohibit the splitting of residential areas among multiple schools. Thus, each of the six areas must be assigned to a single school. (d) Formulate a BIP model for this problem under the current policy of providing bussing for all middle school students who must travel more than approximately a mile. (e) Referring to part (a) explain why that linear programming model and the BIP model just formulated are so different when they are dealing with nearly the same problem. (1) Solve the BIP model formulated in part (d) (EXCEL/R/PYTHON). (g) What is your new resulting recommendation to the school board? (e) Compare the two methods. Pick the "worst solution between parts (a) and (f) from an objective standpoint (i.e. more expensive, more complicated, etc.), and develop an argument as to why the 'worst solution should be chosen. You may choose which solution you believe is worst, but you must first qualify 'why it is worse than the other, then make your argument. Example: option 1 is cheaper (so 'best by $$) but option 2 displaces less students. Remember, this is an argument to management in this case, the Springfield schoolboard), who are not experts in OR! Avoiding technical language is paramount or you will confuse them and get fired, but be thorough enough that they will understand why they must choose your answer instead