I need help

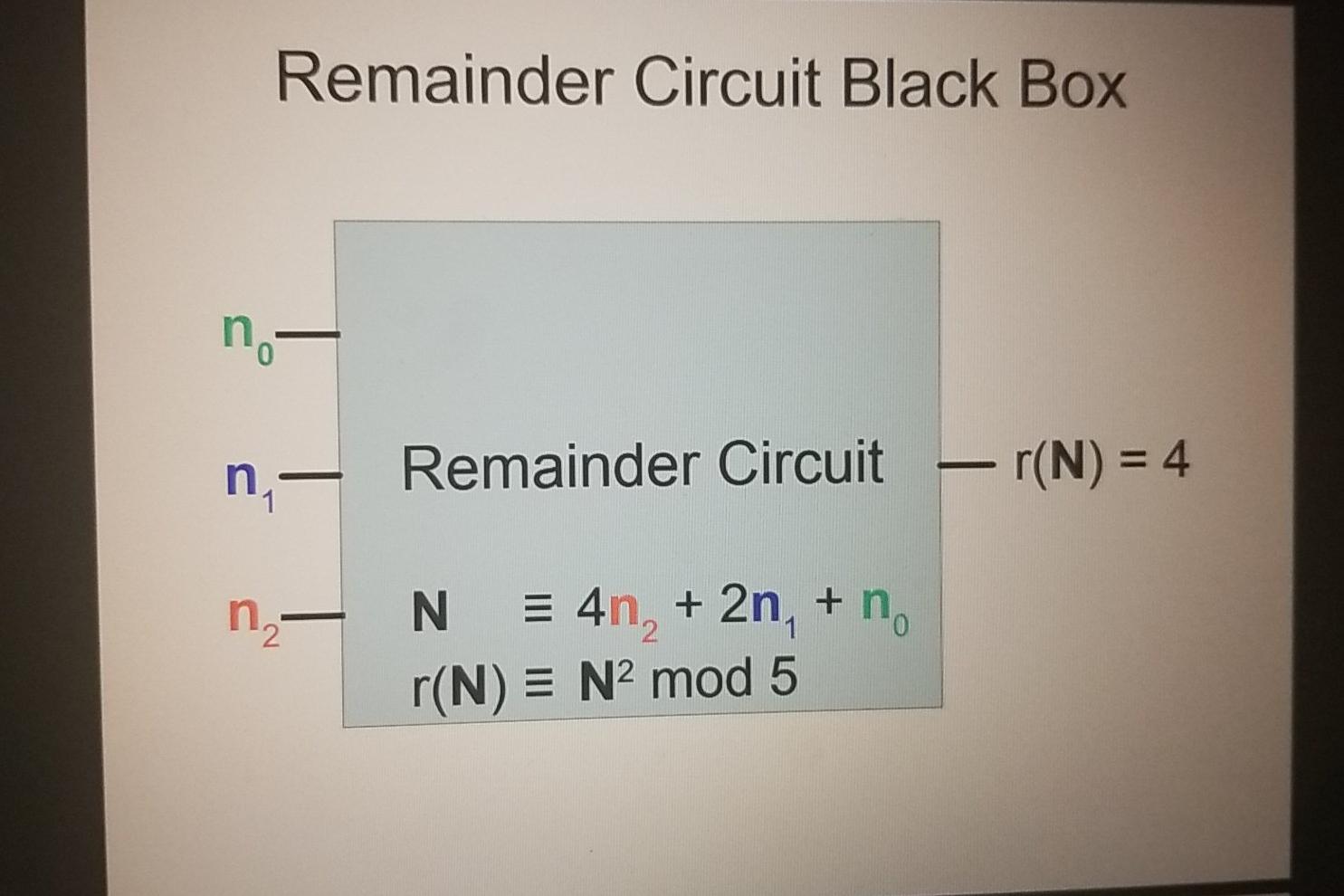
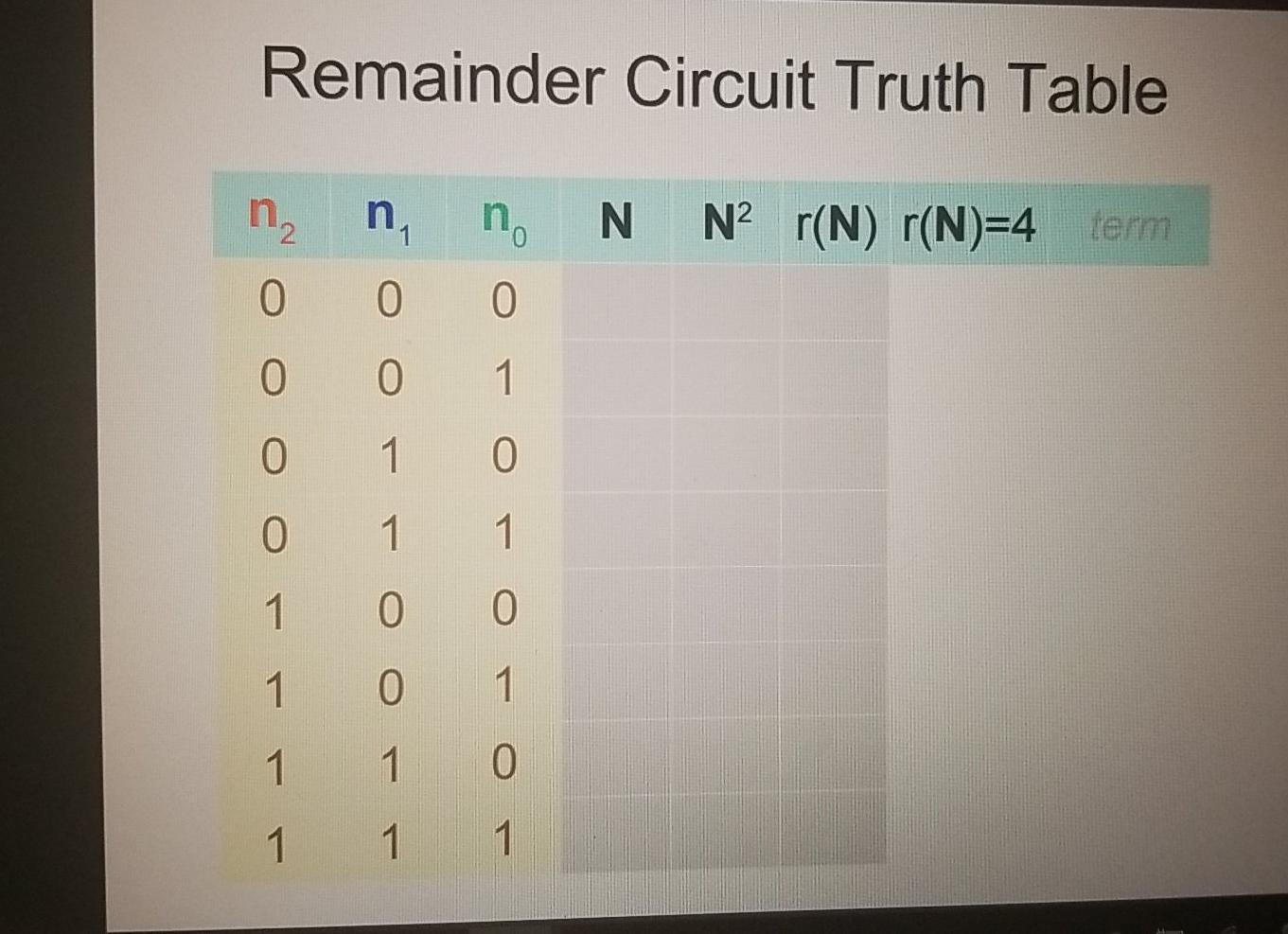
HW 4: Remainder Circuit Design Complete the Combinational Circuit Design process from class to create a circuit that takes a 3-bit Unsigned Integer N as input and has a 1-bit output that is 1 if, and only if, the integer remainder of Na divided by 5 is 4. A Black Box diagam for this circuit has been provided, as has a start on its truth table. Complete this table and derive from it the equivalent Boolean clause. Build (and verify) the circuit for this clause in logisim-evolution. Submit the completed truth table, the Boolean clause, and a .png file of the circuit diagram. Remainder Circuit Black Box no n Remainder Circuit - r(N) = 4 n N = 4n, + 2n + n. r(N) = N2 mod 5 Remainder Circuit Truth Table n n N N2 r(N) r(N)=4 term 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1