I need help with the 3 attached problems, thank you!

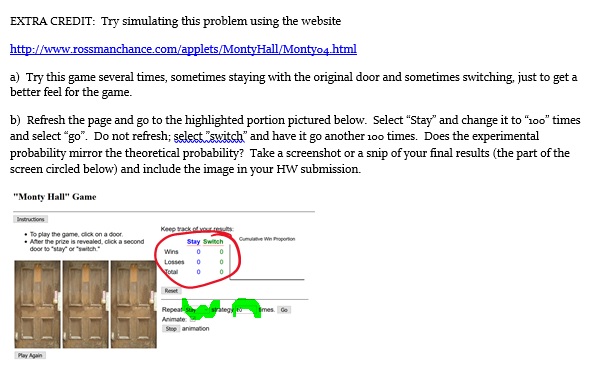
1. In class, we discussed the probability of a family with 2 children having z boys if we know that at least one of the children is a boy. We saw that the probability was 1/3. Consider the following variation of this problem: Suppose a family has 2 children, and you know that at least one of them is a boy born on a Tuesday. What is the probability that both children are boys? This is a more complicated problem. For the one we did in class, we only needed to consider the gender of each child. Now we must consider not only gender, but also day of birth for each child. The answer to this problem is 13/27; I'd like you to discover how to arrive at this answer. Let's begin with the following: a) To find the number of elements in the sample space for a family with 2 children, keeping track of the days on which they were born, we would use the Fundamental Counting Principle. Think of this as a four-part task, and fill in the blanks below: # possibilities for the gender of the first child: # possibilities for the gender of the second child: # possibilities for the day of the week for the birth of the first child: # possibilities for the day of the week for the birth of the second child: How many elements are in this sample spacel. b) Now, in the problem from class, the condition that at least one of the children was a boy reduced the size of our sample space (we threw away the gg possibility.) A similar situation arises in our new problem. For one thing, we again know that at least one child is a boy, so all of the possibilities with 2 girls will be removed from our sample space. In addition, we know that this boy was born on a Tuesday, so now the sample space is reduced to only the possibilities that include a boy born on a Tuesday. There are 27 such possibilities (thus the denominator of the answer provided above.) List these 27 possibilities. Note: one possibility would be bbMT, representing the possibility where both children are boys, the first born on Monday, the second born on Tuesday. c) Look at your list of 27 possibilities and explain why the answer to our problem is 13/27.2. A very famous probability puzzle is the Monty Hall problem. Monty was the host of the TV game show Let's Make a Deal. In one of the games on the show, Monty would give a contestant 3 doors to choose from. Behind one of the doors was a grand prize, perhaps a car, and behind the other a were goats. The contestant chose one of the doors. Then Monty, who knew where the grand prize was, would open one of the other two doors, revealing a goat. He would then ask the contestant if they would like to switch from their original choice of door to the remaining door. a) What is the probability that the contestant chose the door with the grand prize at the beginning of the game? b) After Monty shows the goat behind one of the other doors, what do you think is the probability of the third door (not the one the contestant originally chose) hiding the grand prize? Should the contestant switch? Explain your reasoning Please note: I am only interested in knowing what you think and why, based on what you know of probability theory. The following article discusses this problem in detail and explains the solution in several ways. Please read it - AFTER you have answered parts a & b. http://www.maa.org/external archive/devlin/devlin of oz.html c) After reading the article, are you convinced? Write a short paragraph explaining your thoughts.EXTRA CREDIT: Try simulating this problem using the website http://www.rossmanchance.com/applets/MontyHall/Montyo4.html a) Try this game several times, sometimes staying with the original door and sometimes switching, just to get a better feel for the game. b) Refresh the page and go to the highlighted portion pictured below. Select "Stay" and change it to "100" times and select "go". Do not refresh; select "switch" and have it go another 100 times. Does the experimental probability mirror the theoretical probability? Take a screenshot or a snip of your final results (the part of the screen circled below) and include the image in your HW submission. "Monty Hall" Game . To play the game. click on a door . We the prize is revealed. click a second Stay Switch Wins ToMi Times. Go Animate Jap animation