I need help with these; on the first one I only need help with parts a and d.

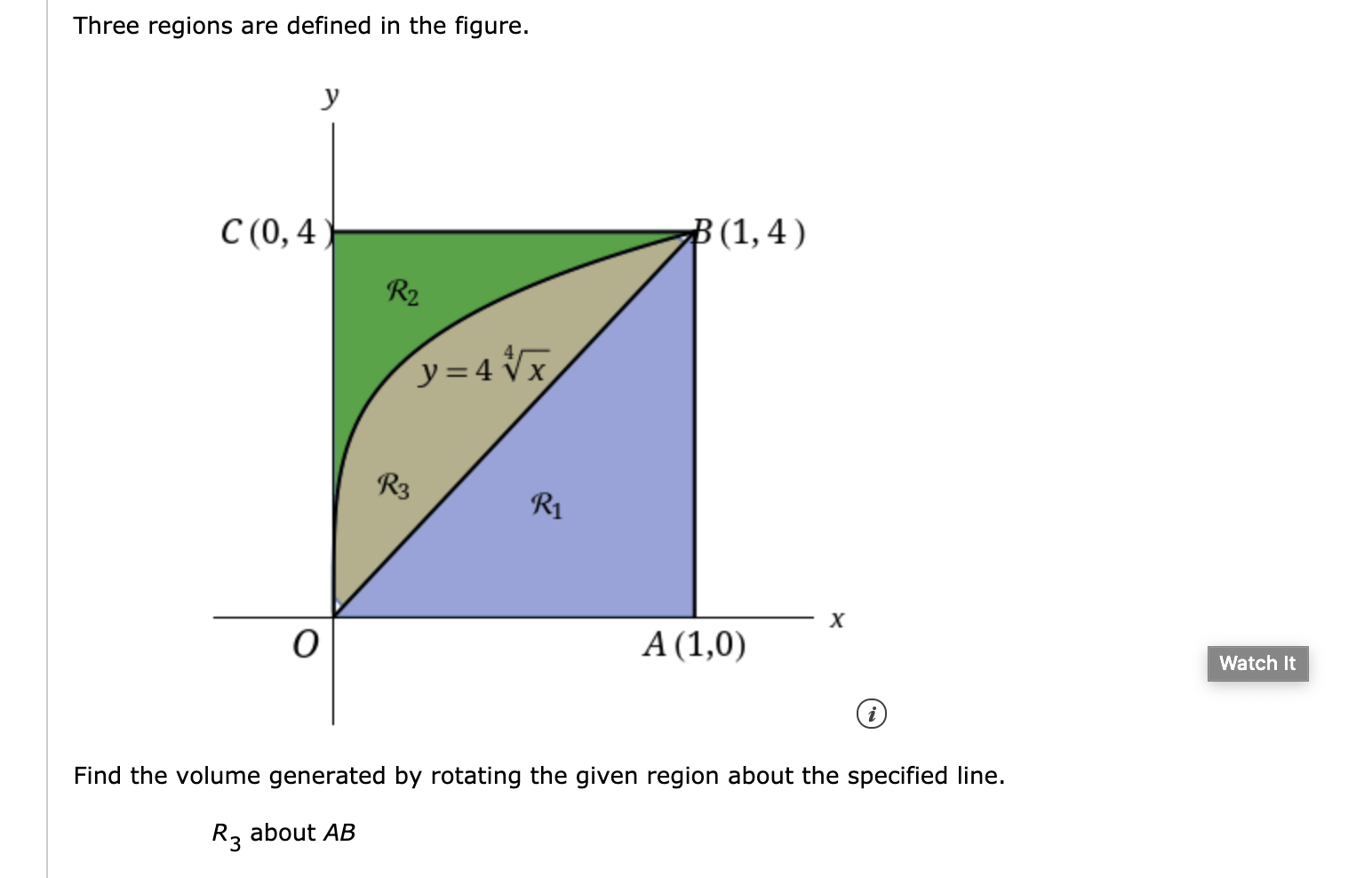
Three regions are defined in the figure. y C(0,4 (1.4) 0 \"1"\" 69 Find the volume generated by rotating the given region about the specified line. R3 about AB A particle moves along a horizontal line so that its position at time t, t Z 0, is given by s(t) = t3 9t2 + 24f 10, where t is measured in seconds and s in meters. (a) Find the average velocity (in m/s) of the particle over the interval [0, 2]. I: m Does the particle travel with this velocity at any instant on the interval? Explain the reason for your answer. The distance function ---Select-- V| continuous on 0, 2]. The distance function differentiable on (0, 2). SO the Mean Value Theorem aPPIY- Therefore, the instantaneous velocity of the particle ---Select- v equal the average velocity at some instant on the interval. (b) Write an expression for v(t), the velocity of the particle at time t. v(t) = (c) Find the values of t (in s) for which the velocity is zero. (Enter your answers as a comma-separated list.) t= s (d) Using your answer from part (c), explain why there must be a time t at which the acceleration is zero. The velocity function Select v continuous on [2, 4]. The velocity function -Selec1 v differentiable on (2, 4). So the Mean Value Theorem apply. The average acceleration of the interval is equal to |:] m/sz. Therefore, the instantaneous acceleration of the particle ---Select--- V equal 0 m/s2 at some instant on the interval. Find this value (in s)