I only need an answer to the second half (bolded half) of this problem, Part a is the correct answer. i've attached my incorrect submissions so far.

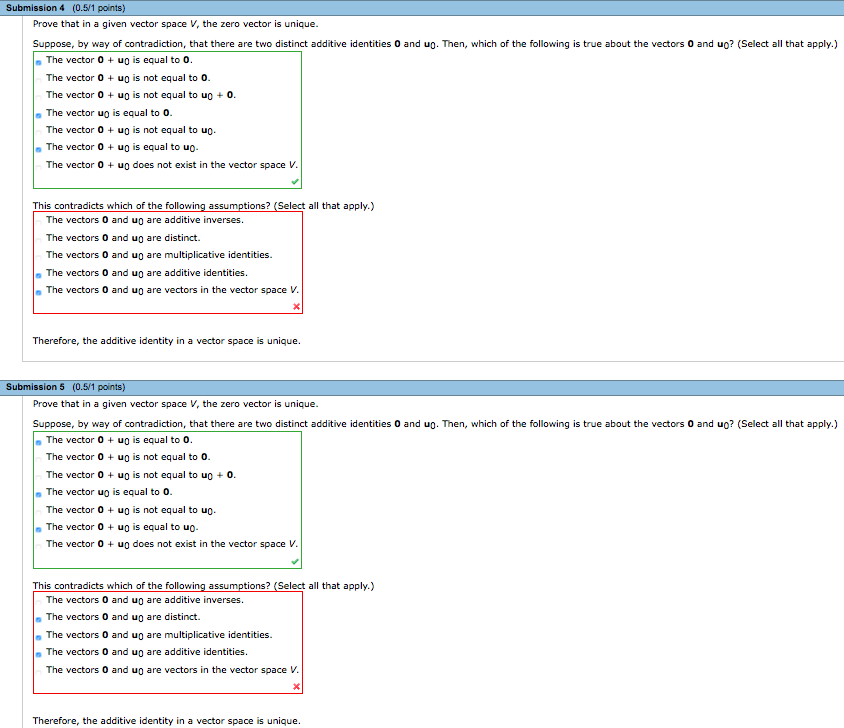
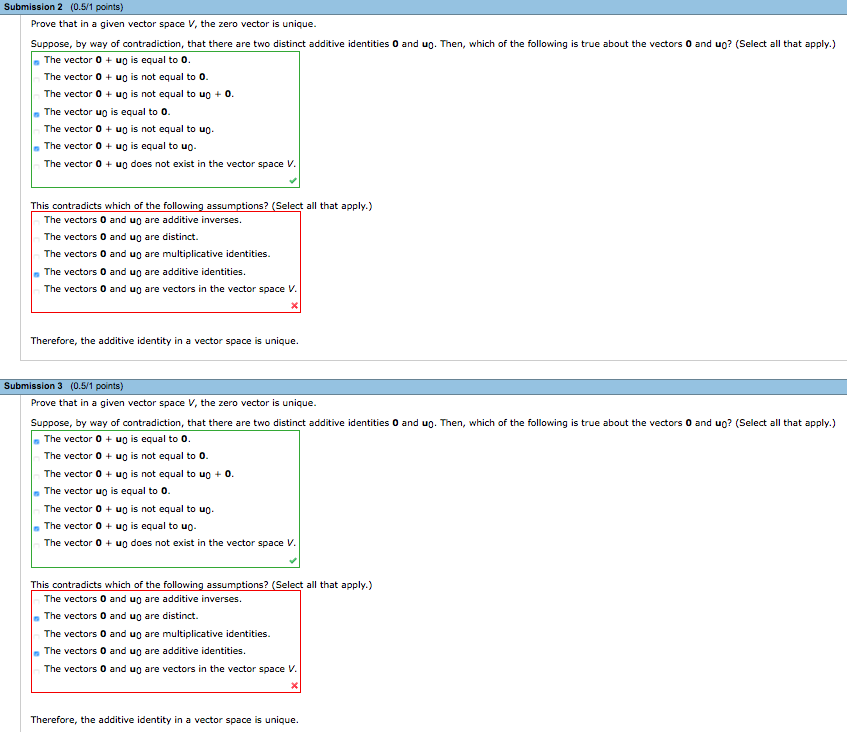
Prove that in a given vector spaceV, the zero vector is unique.

A) Suppose, by way of contradiction, that there are two distinct additive identities0andu₀. Then, which of the following is true about the vectors0andu₀? (Select all that apply.)

The vector0+u₀is equal to0.

The vectoru₀is equal to0.

The vector0+u₀is equal tou₀.

This contradicts which of the following assumptions? (Select all that apply.)

The vectors0andu₀are additive inverses.

The vectors0andu₀are distinct.

The vectors0andu₀are multiplicative identities.

The vectors0andu₀are additive identities.

The vectors0andu₀are vectors in the vector spaceV.

Therefore, the additive identity in a vector space is unique.

Submission (0.5/1 points) 2 Wednesday, October 25 2017 01:37 PM EDT Prove that in a given vector space V, the zero vector is unique. Suppose, by way of contradiction, that there are two distinct additive identities 0 and u0. Then, which of the following is true about the vectors 0 and u0? (Select all that apply.) The vector 0 + u0 is equal to 0. The vector 0 + u0 is not equal to 0. The vector 0 + u0 is not equal to u0 + 0. The vector u0 is equal to 0. The vector 0 + u0 is not equal to u0. The vector 0 + u0 is equal to u0. The vector 0 + u0 does not exist in the vector space V. This contradicts which of the following assumptions? (Select all that apply.) The vectors 0 and u0 are additive inverses. The vectors 0 and u0 are distinct. The vectors 0 and u0 are multiplicative identities. The vectors 0 and u0 are additive identities. The vectors 0 and u0 are vectors in the vector space V. Therefore, the additive identity in a vector space is unique. Submission (0.5/1 points) 3 Wednesday, October 25 2017 01:37 PM EDT Prove that in a given vector space V, the zero vector is unique. Suppose, by way of contradiction, that there are two distinct additive identities 0 and u0. Then, which of the following is true about the vectors 0 and u0? (Select all that apply.) The vector 0 + u0 is equal to 0. The vector 0 + u0 is not equal to 0. The vector 0 + u0 is not equal to u0 + 0. The vector u0 is equal to 0. The vector 0 + u0 is not equal to u0. The vector 0 + u0 is equal to u0. The vector 0 + u0 does not exist in the vector space V. This contradicts which of the following assumptions? (Select all that apply.) The vectors 0 and u0 are additive inverses. The vectors 0 and u0 are distinct. The vectors 0 and u0 are multiplicative identities. The vectors 0 and u0 are additive identities. The vectors 0 and u0 are vectors in the vector space V. Therefore, the additive identity in a vector space is unique. Submission (0.5/1 points) 4 Wednesday, October 25 2017 01:43 PM EDT Prove that in a given vector space V, the zero vector is unique. Suppose, by way of contradiction, that there are two distinct additive identities 0 and u0. Then, which of the following is true about the vectors 0 and u0? (Select all that apply.) The vector 0 + u0 is equal to 0. The vector 0 + u0 is not equal to 0. The vector 0 + u0 is not equal to u0 + 0. The vector u0 is equal to 0. The vector 0 + u0 is not equal to u0. The vector 0 + u0 is equal to u0. The vector 0 + u0 does not exist in the vector space V. This contradicts which of the following assumptions? (Select all that apply.) The vectors 0 and u0 are additive inverses. The vectors 0 and u0 are distinct. The vectors 0 and u0 are multiplicative identities. The vectors 0 and u0 are additive identities. The vectors 0 and u0 are vectors in the vector space V. Therefore, the additive identity in a vector space is unique. Submission (0.5/1 points) 5 Wednesday, October 25 2017 01:44 PM EDT Prove that in a given vector space V, the zero vector is unique. Suppose, by way of contradiction, that there are two distinct additive identities 0 and u0. Then, which of the following is true about the vectors 0 and u0? (Select all that apply.) The vector 0 + u0 is equal to 0. The vector 0 + u0 is not equal to 0. The vector 0 + u0 is not equal to u0 + 0. The vector u0 is equal to 0. The vector 0 + u0 is not equal to u0. The vector 0 + u0 is equal to u0. The vector 0 + u0 does not exist in the vector space V. This contradicts which of the following assumptions? (Select all that apply.) The vectors 0 and u0 are additive inverses. The vectors 0 and u0 are distinct. The vectors 0 and u0 are multiplicative identities. The vectors 0 and u0 are additive identities. The vectors 0 and u0 are vectors in the vector space V. Therefore, the additive identity in a vector space is unique. Prov2 that 'I1 2 given vector space v, the zero vector ls unique. Suppose, by way of mntradidion, that there are two disti1ct additive identies It and Ila. T|i2I1I which of the following is true about the vectors II and or]? (Seteti all that apply-J I 1112vect3orII + Ila isequal toll. 1112vect3orII + Ila is notequal loll. 1112vect3orII + Ila is notequal loua +0. I 1112vect3orm isequa] loll. 1112vect1orII + Ila is notequal long. I 1112vect1or + Ila isequal toIIa. 1112vect1or+|ladoesnotexisti1theveotorspace LI\". 1' Thisoono'adlcts whim of the toltowi assu tlons? Select all that apply.) 1112 vectors It a1d Ila are aodltlve iwersau. 1112 vectors It a1d Ila are dlstinot. 1112 vectors It 31d Ila are multiplioative identities. I 1112 vectors It a1d Ila are aodltlve identltl. I 1112vect3orslla1dllaareveotorsi1thevednrspac2 if. X Therefore, the additlue Identity in a vector space is unlque. Prove that i1 a aim vector space if, the zero vector ls unique. Suppose, bywayofmntradidion, that there are twnoisthct additive identitieslt and Ila. T|i2I1I which otthe following is true about the vectors Band or]? (Seteti all that apply-J I 1112vect1orB+IlaisequaltoIL 1112vectJorII+IlaismteoualtoD. 1112vect1orB+IlaisrvoteoualtoIIa+D. I 1112vect3ormisequal toll. 1112vect1orB+IlaisrvoteoualtoIIa. I 1112vectJorII+IlaisequaltoIIu. 1112vect3orlI+Iladonesnotexisti1thevednrspace l-I'. If Thisoono'adlcts whim of the toltowi assu tlons? Select all that apply.) 1112 vectors 0 a1d Ila are addltlve iwers. I 1112 vectnors III and Ila are dlstinct. I 1112 vectors 0 a1d Ila are multiplioative identies. I 1112 vectnors III and Ila are aodltlue identltlu. 1112vect3orslla1dllaareveotorsi1thevednrspac2 if. X Therefore, the additlve Identity 'I1 a vector space is unlque. Pun-re that in a given uecbor space If, the zemveclzor ls unique. Suppose, bywaycfcnnlraudidiun, Ii1a|t there are tw'ndistinct additive identitiesll and ua. Then, which plthe follcwing is line about the vectors Band ua? [Select all Ii1at apply.) I 11121rechur+|laisequaltnm 11121rednr+llaisrwtequaltull 11121rednr+llaisrwtequaltuua+l I 11121rechurm isequal tall. 11121rechur+|laisnctequaitcua. I 11121rechur+|laisequaltnua. 1112ved3urlI+Iladnesnotexistil1thevectcrspacelu I This ccnbadlds whim cf the following EESUWHOFE? {Select all that apply.) 1112 vechurs II a1d Ila are addltlue 'IW'EfS-E. 1112 vechurs II a1d Ila are dlsh'nct. 1112 vechurs II a1d Ila are multiplicative identities. I 1112 vednrs II and Ila are addltlue identltl. 1112ved3ursllal1dllaare Hednrshreuednrspace If. x Therefore, the additlve Idenlity in a Better space is unlque. Prmrethat in aaiven uecbor space If, the zemveclzor ls unique. Suppose, bywaycfcnnlraudidiun, Ii1a|t there are tw'ndistinct additive identitiesll and ua. Then, which plthe follcwing is line about the vectors Band ua? [Select all Ii1at apply.) I 11121r2dnr+llaisequaltnll 11121rednr+llaisrwtequaltull 11121rechur+uaisnatequaituua+m I 11121rechurmisequal tall. 1112vec|3urlI+Ilaisnctequaltuug. I 11121|Iednrli+llaisequaltnua. 1112ved3urlI+Iladnesnotexistil1thevectcrspacelu If This cunbadlds whim cf the following assumptlcns? {Select all that anal-[.1 1112 vechurs II a1d Ila are addltlue 'IW'EfS-E. I 1112 vechurs II a1d Ila are dlsh'nct. 11121|Iednrs II and Ila are mulliplicallive identies. I 11121|Iednrs II and Ila are addltlue identltl. 11121Iednrslla1dllaare vednrshthevednrspace if. X Therefore, the additlve Idenlity in a cedar space is unlque