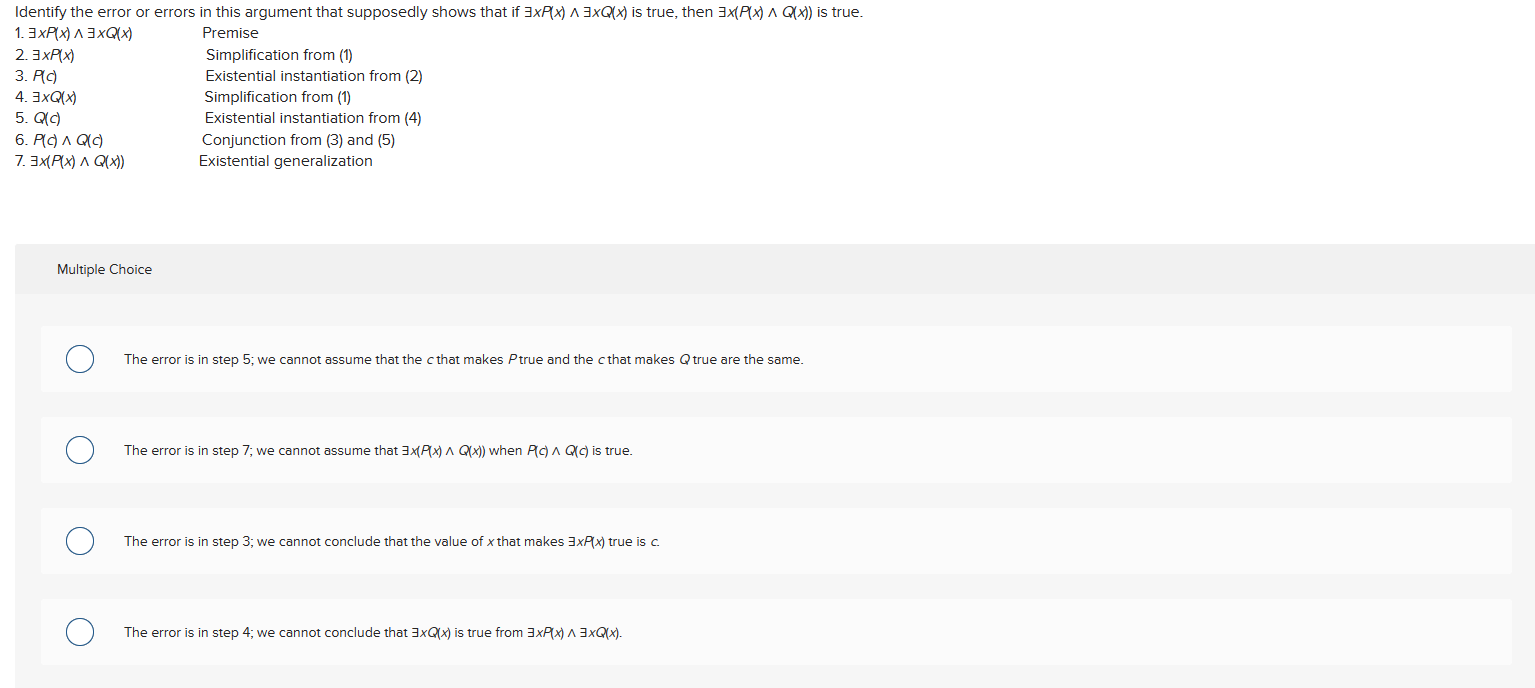
Identify the error or errors in this argument that supposedly shows that if xP(x)xQ(x) is true, then x(P(x)Q(x)) is true. 1. xP(x)xQ(x) Premise 2. xP(x) 3. P(c) Existential instantiation from (2) 4. xQ(x) Simplification from (1) 5. Q(c) Existential instantiation from (4) 6. P(c)Q(c) Conjunction from (3) and (5) 7. x(P(x)Q(x)) Existential generalization Multiple Choice The error is in step 5; we cannot assume that the c that makes P true and the c that makes Q true are the same. The error is in step 7; we cannot assume that x(P(x)Q(x)) when P(c)Q(c) is true. The error is in step 3; we cannot conclude that the value of x that makes xP(x) true is c. The error is in step 4; we cannot conclude that xQ(x) is true from xP(x)xQ(x)