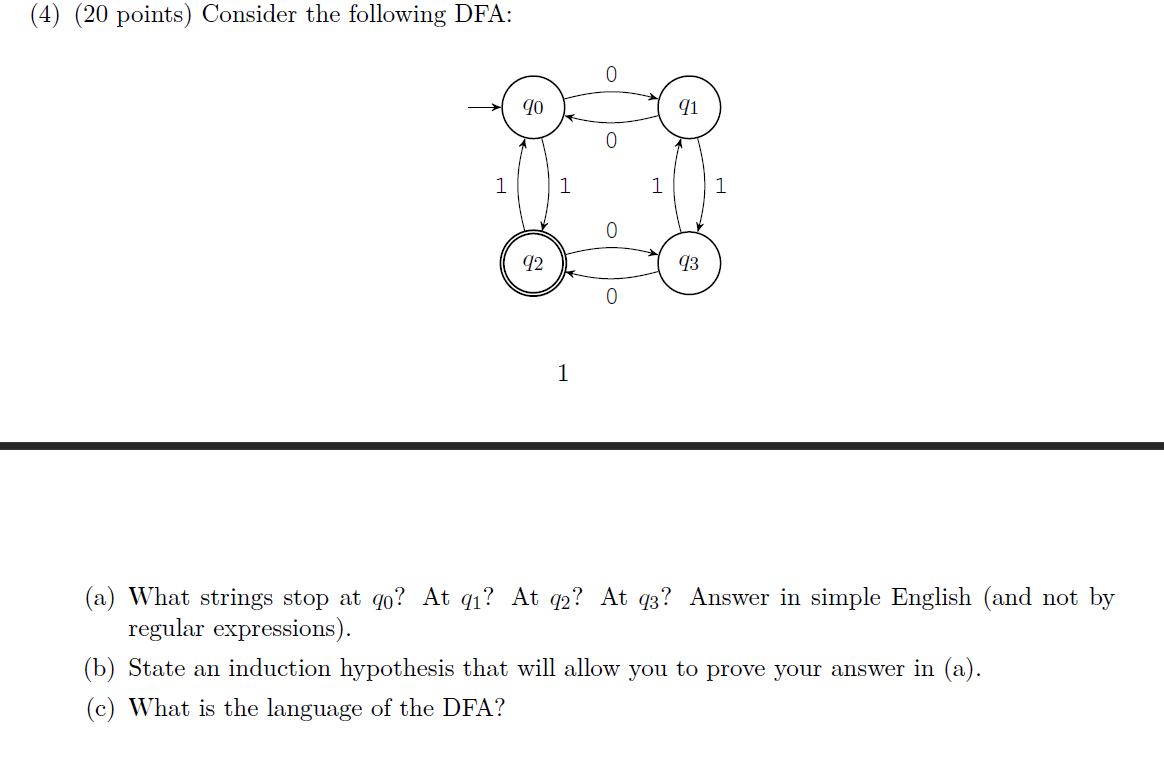
If w is a string, call a string x a subsequence of w if x can be obtained from w by removing zero or more symbols from w. For example, bd and c are both subsequences of bcde. S0x181x2 XmSm for some strings Formally, x = x m is a subsequence of w if w SO,, Sm. Given a language L, define LS = {x|x is a subsequence of some w E L}. That is, LS contains all the subsequences of strings in L. Prove that if L is a regular language, then so is LS. Hint: Regular language is defined recursively. If the desired result is true for simpler regular languages, can you show that it is also true for more complex regular languages? (4) (20 points) Consider the following DFA: 1 90 92 1 1 o 0 0 1 91 93 1 (a) What strings stop at qo? At q? At q2? At q3? Answer in simple English (and not by regular expressions). (b) State an induction hypothesis that will allow you to prove your answer in (a). (c) What is the language of the DFA?