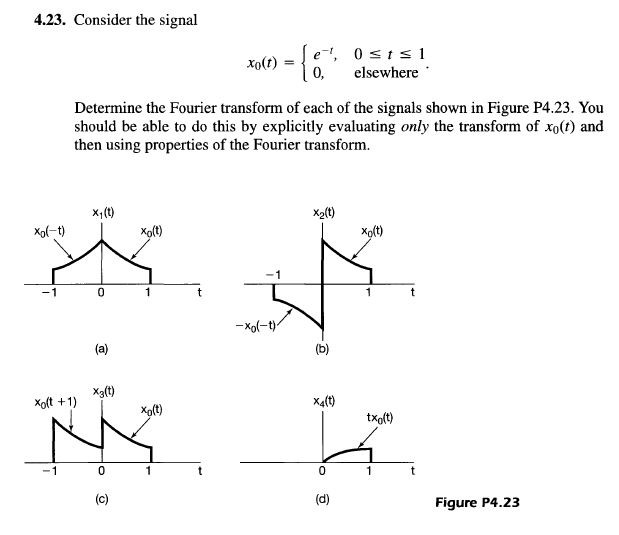
ii. by MATLAB %Homework 2, Problem 2, 4.23(c) cls; clear all; close all; syms t W; %symbolic variables t:time, w: frequency xo(t)= *rectangular Pulse(t-1/2); %Complete xo(t) for ost31 Xo (W)=fourier(xo); %get Fourier transform Xo(W) of xo(t) disp('Xo=') pretty(Xo) %display pretty answer for Xo (W) %4.23 PART C %x(t)=xo(t)+xo (t+1); %Using linearity and time shifting X= ; %Complete X= X. (W)+ (W) disp('4.23 Part c, X=') pretty(x) Show completed MATLAB code above + copy/paste result from the Command window: 4.23. Consider the signal elsewhere Determine the Fourier transform of each of the signals shown in Figure P4.23. You should be able to do this by explicitly evaluating only the transform of xo(t) and then using properties of the Fourier transform. Xy(t) Xa(t) Xol-t Xolt) Xolt) 0 1 1 -X (-) (a) (b) X3(t) Xolt +1) X4(t) Kg(1) txot) - 1 0 1 t (c) (d) Figure P4.23 ii. by MATLAB %Homework 2, Problem 2, 4.23(c) cls; clear all; close all; syms t W; %symbolic variables t:time, w: frequency xo(t)= *rectangular Pulse(t-1/2); %Complete xo(t) for ost31 Xo (W)=fourier(xo); %get Fourier transform Xo(W) of xo(t) disp('Xo=') pretty(Xo) %display pretty answer for Xo (W) %4.23 PART C %x(t)=xo(t)+xo (t+1); %Using linearity and time shifting X= ; %Complete X= X. (W)+ (W) disp('4.23 Part c, X=') pretty(x) Show completed MATLAB code above + copy/paste result from the Command window: 4.23. Consider the signal elsewhere Determine the Fourier transform of each of the signals shown in Figure P4.23. You should be able to do this by explicitly evaluating only the transform of xo(t) and then using properties of the Fourier transform. Xy(t) Xa(t) Xol-t Xolt) Xolt) 0 1 1 -X (-) (a) (b) X3(t) Xolt +1) X4(t) Kg(1) txot) - 1 0 1 t (c) (d) Figure P4.23