I'm tryna get help on these questions I failed during my class work yesterday I need to see what I did wrong

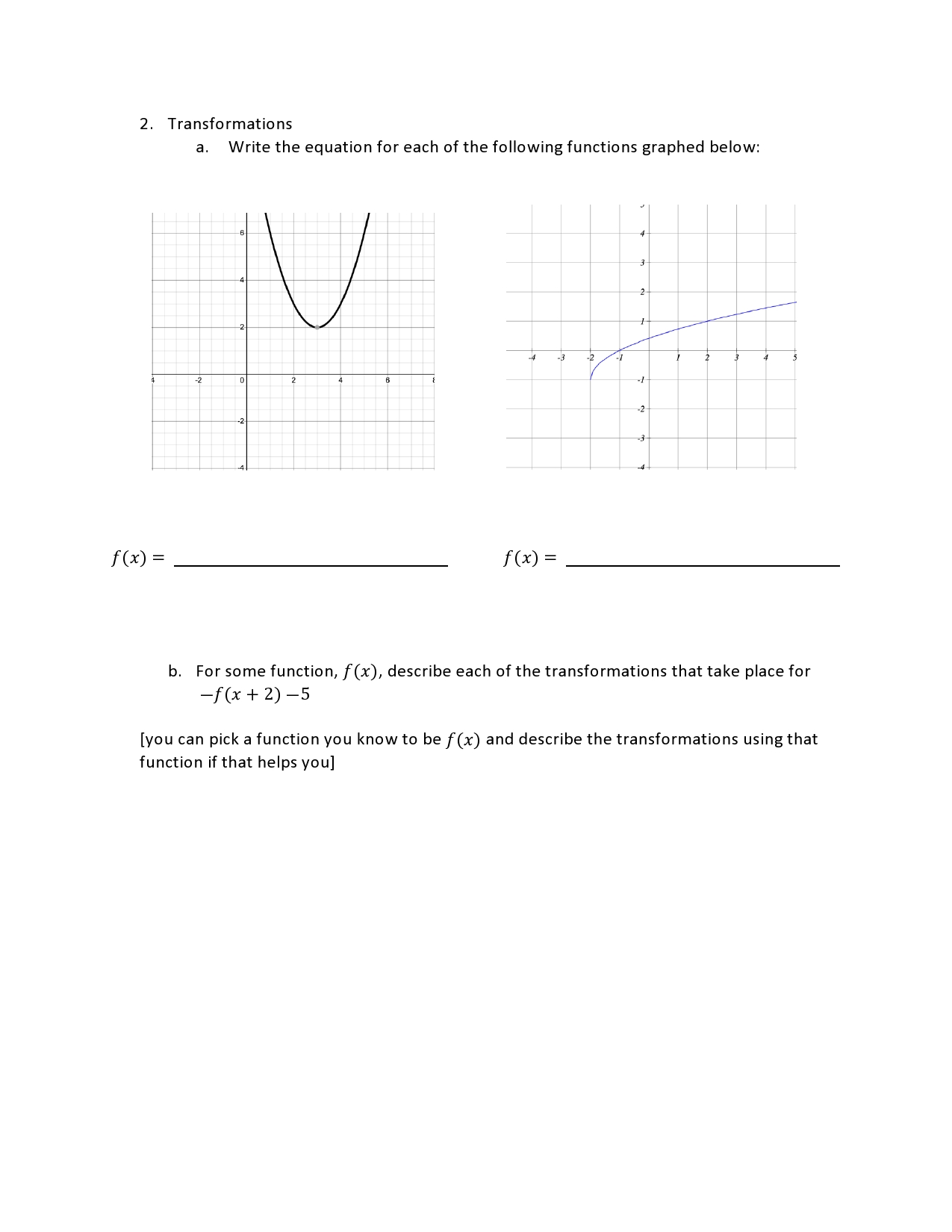
State the domain for each function below using interval notation. Classify the type of equation to decide how to approach finding the domain: a) f(x) = 4x 7 Type of Function: bl 90') = l3x + 1 Type of Function: x2 + 3 Cl h(x) = 7 _ 3x Type of Function: 2. Transformations a. Write the equation for each of the following functions graphed below: f(X)= f(XD= b. For some function, f(x), describe each of the transformations that take place for f(x + 2) 5 [you can pick a function you know to be f(x) and describe the transformations using that function if that helps you] 6x + 8 3. For f(x) = x2 +5x - 4 and g(x) = x a. Calculate f(g( -2)) = b. Calculate g(f( -2)) = 6x + 8 Bonus point, what is the domain of g (x) =- X4. For f(x) = x + 7 and g(x) = x - 3 a. find f(g(x)) and g(f(x)) b. Are the two functions, f(x) and g(x) inverses of each other? Use at least one sentence to explain your answer (no sentence, no points)5. For the function f(x) =x3 4 a. If the point [2, 4} is on the graph of f(x), what is the corresponding point on the graph ofthe inverse function, f_1(x)? The corresponding point on the inverses function is: b. Find the inverse of the function f(x) = x3 4 algebraically: you must show each step in your work Q Show that they are inverse functions by finding f[(f_1(x)) = f_1(f(x)) = x You must show all of your work {at each step}) in order to receive credit