import core

class BstEntry(core.Entry):

def __init__(self, key, value): self._key = key self._value = value self._left = None self._right = None self._parent = None

def get_key(self): return self._key def get_value(self): return self._value def get_left(self): return self._left def get_right(self): return self._right def get_parent(self): return self._parent def set_left(self, node): self._left = node def set_right(self, node): self._right = node def set_parent(self, node): self._parent = node

class BstSortedMap(core.SortedMap): def __init__(self): self._size = 0 self._root = None # attaches the subtree rooted at 'child', to the parent def _attach_left(self, parent, child): if child != None: child.set_parent(parent) if parent != None: parent.set_left(child)

# attaches the subtree rooted at 'child', to the parent def _attach_right(self, parent, child): if child != None: child.set_parent(parent) if parent != None: parent.set_right(child)

################################ # Map ADT methods: ################################ def size(self): return self._size

def is_empty(self): return self._size == 0

def contains_key(self, key): return self.get(key) != None

def get(self, key): return self._get(key, self._root) def _get(self, k, subtree_root): # base case: empty subtree if subtree_root == None: # k isn't in this subtree return None # base case: k matches the key in the current entry if k == subtree_root.get_key(): # TODO: return the value return None # recursive case: k the current entry else: # TODO: return the result of recursing to the right return None

def put(self, key, value): # Replace the subtree rooted at 'root' with # the resulting subtree after doing the put self._root = self._put(key, value, self._root) # Recursive helper method for put # Returns the subtree rooted at entry after performing the put def _put(self, k, v, subtree_root): # base case: the key wasn't in the tree if subtree_root == None: # we have reached a null subtree, where k should be # TODO: create a new entry # TODO: increment the size variable # TODO: return the new entry return None # base case: k matches the one in the current entry elif k == subtree_root.get_key(): # TODO: create a new entry # TODO: attach_left the left child of the current entry to it # TODO: attach_right the right child of the current entry to it # TODO: return the new subtree return None # recursive case: k the current entry else: # TODO: get the subtree resulting from recursing right # TODO: attach that subtree to the current entry # TODO: return the modified entry return None

def remove(self, key): # we will need to return the old value old_value = self.get(key) # Replace the subtree rooted at 'root' with # the resulting subtree after doing the put self._root = self._remove(key, self._root); # return the old value return old_value # Recursive helper method for put # Returns the subtree rooted at entry after performing the put def _remove(self, k, subtree_root): # base case: the key wasn't in the subtree if subtree_root == None: # nothing to do return None # recursive case: k the current entry elif k > subtree_root.get_key(): # get the subtree resulting from recursing right new_right = self._remove(k, subtree_root.get_right()) # attach that subtree to the current entry self._attach_right(subtree_root, new_right) # the subtree's root itself is unchanged, return it return subtree_root # base case: k == the current entry else: # found, decrement size self._size -= 1 # case 1: no right child if subtree_root.get_right() == None: # return left child to be attached, no other modifications # required return subtree_root.get_left() # case 2: no left child elif subtree_root.get_left() == None: # return right child to be attached, no other modifications # required return subtree_root.get_right() # case 3: left and right child else: # get inorder successor succ = self.higherEntry(k) # successor's right child should take place of successor new_succ = succ.get_right() if succ == succ.get_parent().get_left(): self._attach_left(succ.get_parent(), new_succ) else: self._attach_right(succ.get_parent(), new_succ) # create copy of successor to replace subtree root replacement = BstEntry(succ.get_key(), succ.get_value()) self._attach_left(replacement, subtree_root.get_left()) self._attach_right(replacement, subtree_root.get_right()) # inform caller of replacement subtree root to be attached return replacement

############# # SortedMap ADT methods: ############# def first_entry(self): raise NotImplementedError

def last_entry(self): raise NotImplementedError

def ceiling_entry(self, key): raise NotImplementedError

def floor_entry(self, key): raise NotImplementedError

def lower_entry(self, key): raise NotImplementedError

def higher_entry(self, key): return self._higher_entry(key, self._root, None) def _higher_entry(self, k, subtree_root, upper_bound): # base case: empty subtree if subtree_root == None: return upper_bound # recursive case: k = the current entry else: # upper_bound's key still least upper bound return self._higher_entry(k, subtree_root.get_right(), upper_bound)

def main(): # This function is here for you to optionally use for your own # testing / running. This function will NOT be tested. print("Running the main function in bst_sorted_map.py") pass

if __name__ == "__main__": main()

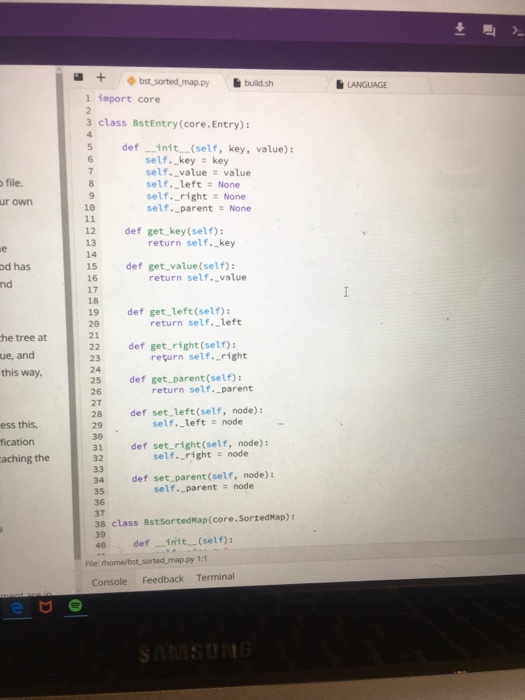
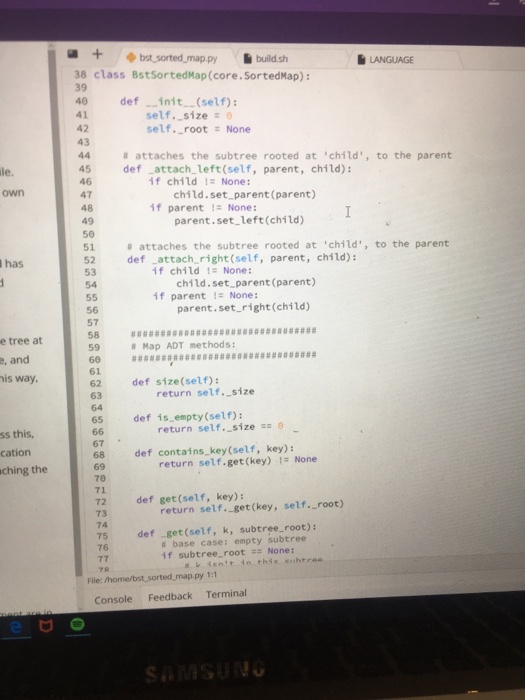
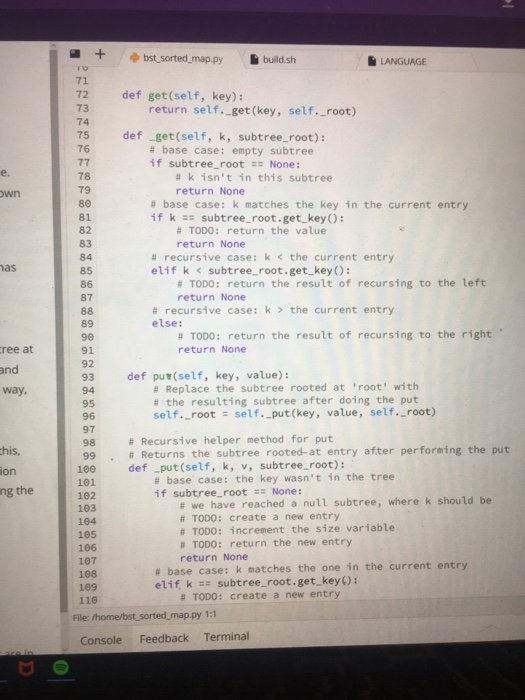
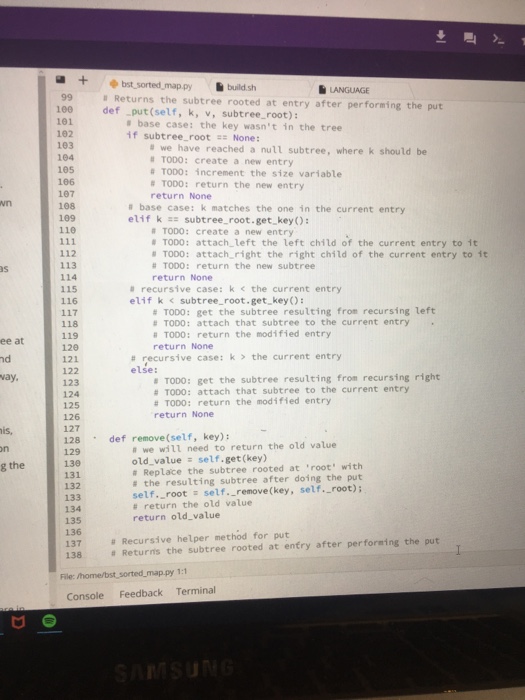Implementing the get and put function on a binary search tree in python . I have been given the skeleton code. I am especially having trouble recurring .

editable code: