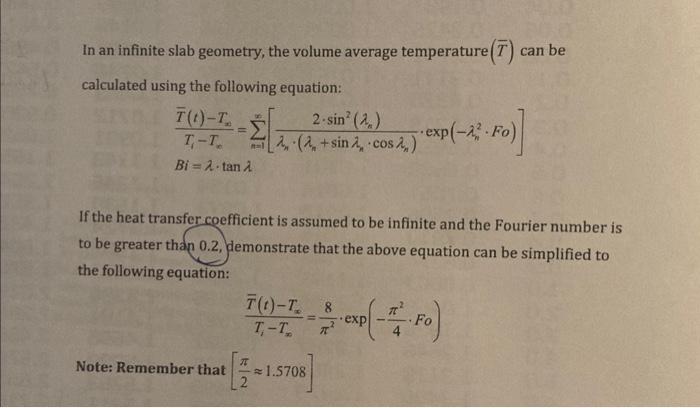
In an infinite slab geometry, the volume average temperature (T) can be calculated using the following equation: TiTnT(t)Tn=n=1[n(n+sinncosn)2sin2(n)exp(n2Fo)]Bi=tan If the heat transfer coefficient is assumed to be infinite and the Fourier number is to be greater than 0.2, demonstrate that the above equation can be simplified to the following equation: TiTT(t)T=28exp(42F0) Note: Remember that [21.5708] In an infinite slab geometry, the volume average temperature (T) can be calculated using the following equation: TiTnT(t)Tn=n=1[n(n+sinncosn)2sin2(n)exp(n2Fo)]Bi=tan If the heat transfer coefficient is assumed to be infinite and the Fourier number is to be greater than 0.2, demonstrate that the above equation can be simplified to the following equation: TiTT(t)T=28exp(42F0) Note: Remember that [21.5708]