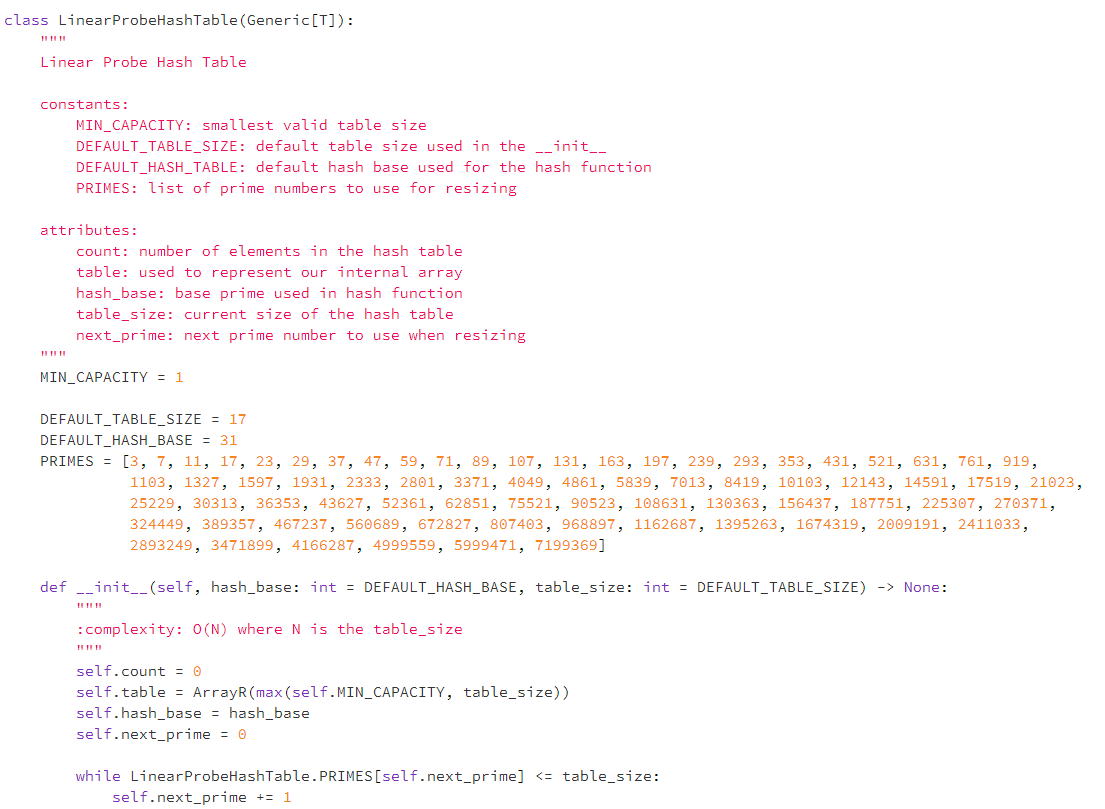
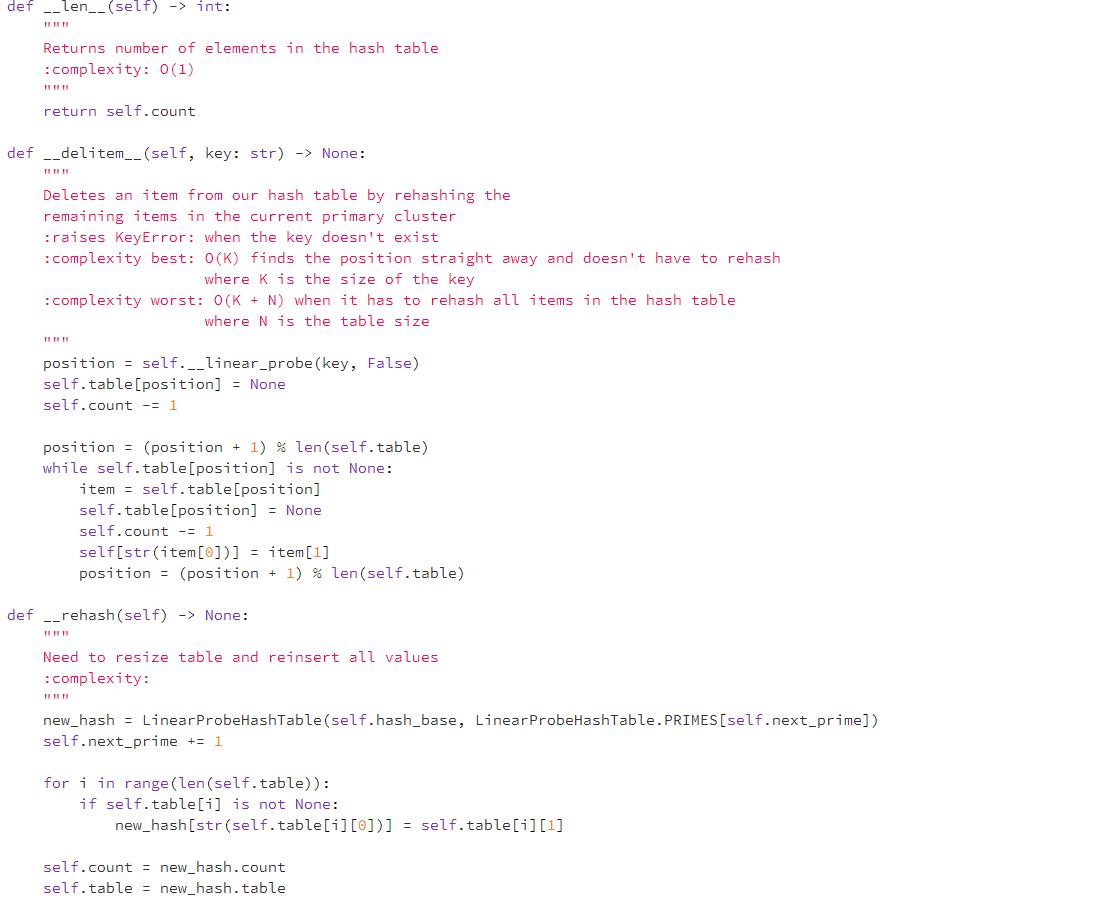
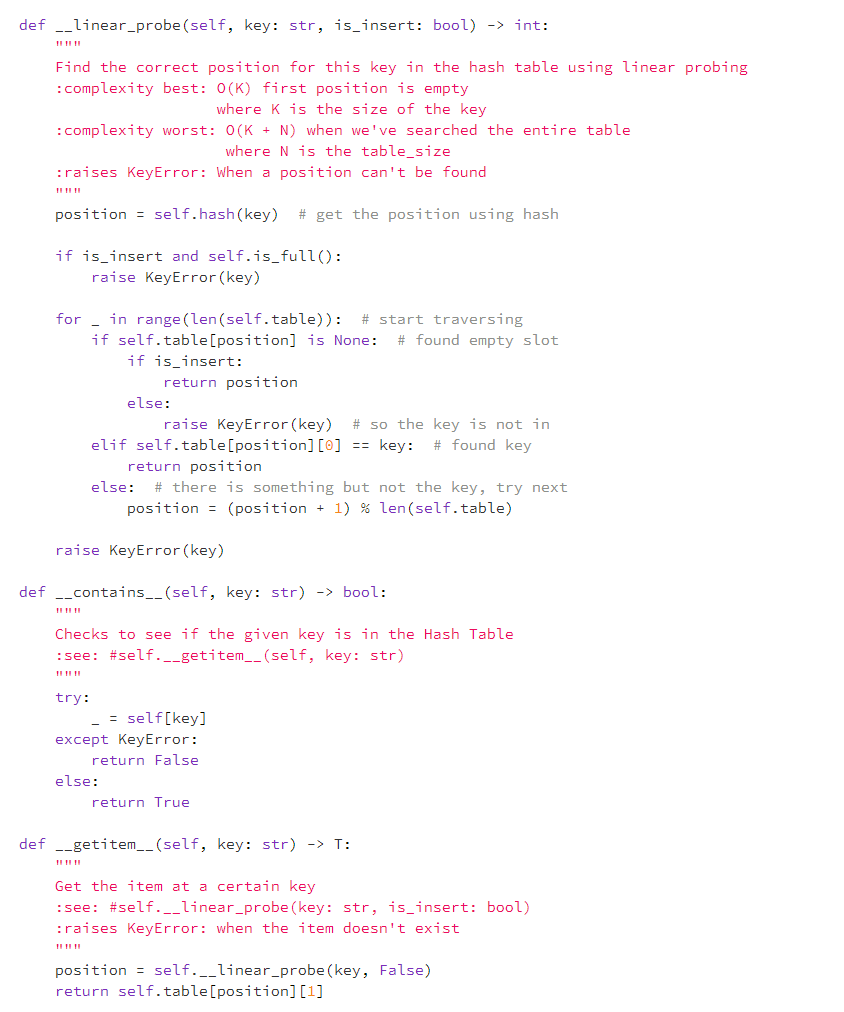
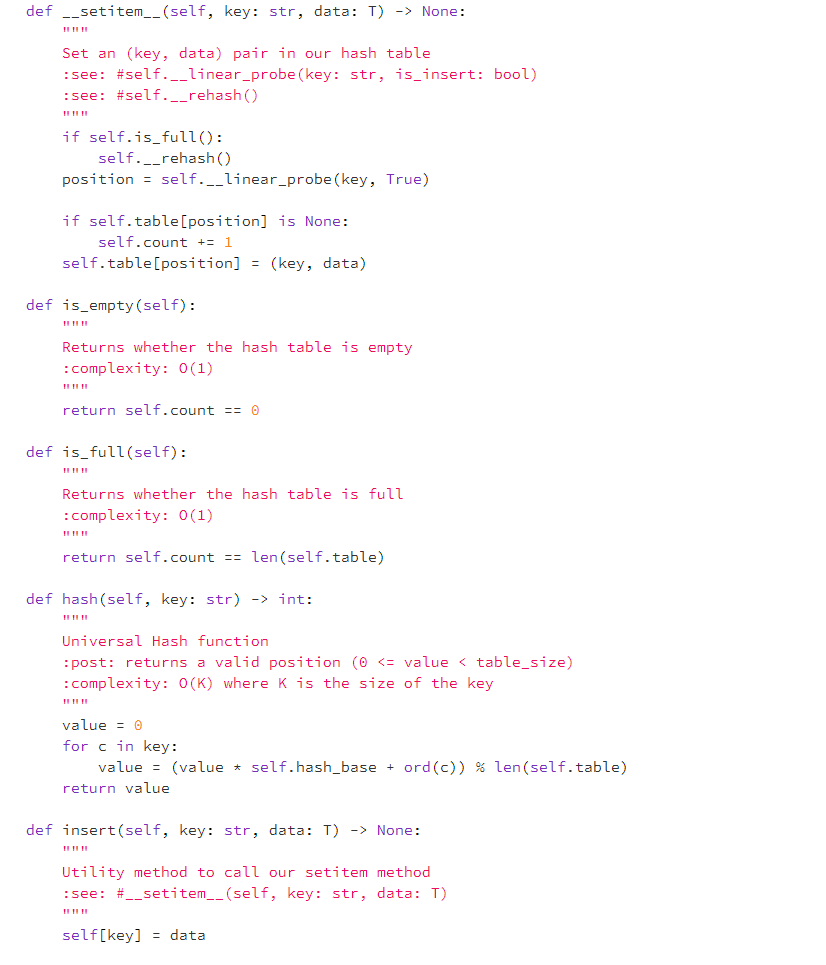
Question: In Python please In hash_table.py: Modify the LinearProbeHashTable class with a method statistics(self) -> Tuple, which returns a tuple (collision_count, probe_total, probe_max, rehash_count), consisting of

![(Generic[T]): Linear Probe Hash Table constants: MIN_CAPACITY: smallest valid table size DEFAULT_TABLE_SIZE:](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66f00955b233f_06166f009555ecd5.jpg)
In Python please
In hash_table.py: Modify the LinearProbeHashTable class with a method statistics(self) -> Tuple, which returns a tuple (collision_count, probe_total, probe_max, rehash_count), consisting of o the total number of collisions, o the sum of all the probe chain lengths, o the length of the longest probe chain, o the number of times rehash has been called. class LinearProbeHashTable (Generic[T]): Linear Probe Hash Table constants: MIN_CAPACITY: smallest valid table size DEFAULT_TABLE_SIZE: default table size used in the __init__ DEFAULT_HASH_TABLE: default hash base used for the hash function PRIMES: list of prime numbers to use for resizing attributes: count: number of elements in the hash table table: used to represent our internal array hash_base: base prime used in hash function table_size: current size of the hash table next_prime: next prime number to use when resizing MIN_CAPACITY = 1 DEFAULT_TABLE_SIZE = 17 DEFAULT_HASH_BASE = 31 PRIMES = [3, 7, 11, 17, 23, 29, 37, 47, 59, 71, 89, 107, 1, 163, 197, 239, 293, 53, 31, 521, 31, 76 919, 1103, 1327, 1597, 1931, 2333, 2801, 3371, 4049, 4861, 5839, 7013, 8419, 10103, 12143, 14591, 17519, 21023, 25229, 30313, 36353, 43627, 52361, 62851, 75521, 90523, 108631, 130363, 156437, 187751, 225307, 270371, 324449, 389357, 467237, 560689, 672827, 807403, 968897, 1162687, 1395263, 1674319, 2009191, 2411033, 2893249, 3471899, 4166287, 4999559, 5999471, 7199369] def __init__(self, hash_base: int = DEFAULT_HASH_BASE, table_size: int = DEFAULT_TABLE_SIZE) -> None: :complexity: 0(N) where N is the table_size self.count = 0 self.table = ArrayR(max(self.MIN_CAPACITY, table_size)) self.hash_base = hash_base self.next_prime = 0 while Linear ProbeHashTable.PRIMES[self.next_prime] int: Returns number of elements in the hash table :complexity: 0(1) return self.count def __delitem__(self, key: str) -> None: Deletes an item from our hash table by rehashing the remaining items in the current primary cluster :raises KeyError: when the key doesn't exist :complexity best: O(K) finds the position straight away and doesn't have to rehash where K is the size of the key :complexity worst: O(K + N) when it has to rehash all items in the hash table where N is the table size position = self.__linear_probe (key, False) self.table[position] = None self.count -= 1 position = (position + 1) % len(self.table) while self.table[position] is not None: item = self.table[position] self.table[position] = None self.count -= 1 self[str(item [0])] = item[1] position = (position + 1) % len(self.table) def __rehash(self) -> None: Need to resize table and reinsert all values :complexity: new_hash = Linear ProbeHashTable (self.hash_base, LinearProbeHashTable. PRIMES[self.next_prime]) self.next_prime += 1 for i in range (len(self.table)): if self.table[i] is not None: new_hash(str(self.table[i][0])] = self.table[i][1] self.count = new_hash.count self. table = new_hash. table def __linear_probe (self, key: str, is_insert: bool) -> int: Find the correct position for this key in the hash table using linear probing :complexity best: O(K) first position is empty where K is the size of the key :complexity worst: O(K + N) when we've searched the entire table where N is the table_size :raises KeyError: When a position can't be found position = self.hash (key) # get the position using hash if is_insert and self.is_full(): raise KeyError(key) for in range (len (self.table)): # start traversing if self.table[position] is None: # found empty slot if is_insert: return position else: raise KeyError(key) # so the key is not in elif self.table[position][0] == key: # found key return position else: # there is something but not the key, try next position = (position + 1) % len(self.table) raise KeyError(key) def __contains__(self, key: str) -> bool: Checks to see if the given key is in the Hash Table see: #self.__getitem__(self, key: str) try: = self[key] except KeyError: return false else: return True def --getitem__(self, key: str) -> T: Get the item at a certain key :see: #self.__linear_probe (key: str, is_insert: bool) :raises KeyError: when the item doesn't exist position = self.__linear_probe (key, False) return self.table[position][1] def setitem__(self, key: str, data: 1) -> None: Set an (key, data) pair in our hash table see: #self.__linear_probe (key: str, is_insert: bool) :see: #self.__rehash() if self.is_full(): self.__rehash) position = self.__linear_probe (key, True) if self.table[position] is None: self.count += 1 self.table[position] = (key, data) def is_empty(self): Returns whether the hash table is empty :complexity: 0(1) return self.count == 0 def is_full(self): Returns whether the hash table is full :complexity: 0(1) return self.count == len(self.table) def hash(self, key: str) -> int: Universal Hash function post: returns a valid position (0 None: Utility method to call our setitem method :see: #__setitem__(self, key: str, data: T) self[key] = data def __str__(self) -> str: Returns all they key/value pairs in our hash table (no particular order) :complexity: 0(N) where N is the table size 24 25 26 27 08 29 20 1 2 3 24 result = " for item in self.table: if item is not None: (key, value) = item result += "(" + str(key) + return result + str(value) + ") " In hash_table.py: Modify the LinearProbeHashTable class with a method statistics(self) -> Tuple, which returns a tuple (collision_count, probe_total, probe_max, rehash_count), consisting of o the total number of collisions, o the sum of all the probe chain lengths, o the length of the longest probe chain, o the number of times rehash has been called. class LinearProbeHashTable (Generic[T]): Linear Probe Hash Table constants: MIN_CAPACITY: smallest valid table size DEFAULT_TABLE_SIZE: default table size used in the __init__ DEFAULT_HASH_TABLE: default hash base used for the hash function PRIMES: list of prime numbers to use for resizing attributes: count: number of elements in the hash table table: used to represent our internal array hash_base: base prime used in hash function table_size: current size of the hash table next_prime: next prime number to use when resizing MIN_CAPACITY = 1 DEFAULT_TABLE_SIZE = 17 DEFAULT_HASH_BASE = 31 PRIMES = [3, 7, 11, 17, 23, 29, 37, 47, 59, 71, 89, 107, 1, 163, 197, 239, 293, 53, 31, 521, 31, 76 919, 1103, 1327, 1597, 1931, 2333, 2801, 3371, 4049, 4861, 5839, 7013, 8419, 10103, 12143, 14591, 17519, 21023, 25229, 30313, 36353, 43627, 52361, 62851, 75521, 90523, 108631, 130363, 156437, 187751, 225307, 270371, 324449, 389357, 467237, 560689, 672827, 807403, 968897, 1162687, 1395263, 1674319, 2009191, 2411033, 2893249, 3471899, 4166287, 4999559, 5999471, 7199369] def __init__(self, hash_base: int = DEFAULT_HASH_BASE, table_size: int = DEFAULT_TABLE_SIZE) -> None: :complexity: 0(N) where N is the table_size self.count = 0 self.table = ArrayR(max(self.MIN_CAPACITY, table_size)) self.hash_base = hash_base self.next_prime = 0 while Linear ProbeHashTable.PRIMES[self.next_prime] int: Returns number of elements in the hash table :complexity: 0(1) return self.count def __delitem__(self, key: str) -> None: Deletes an item from our hash table by rehashing the remaining items in the current primary cluster :raises KeyError: when the key doesn't exist :complexity best: O(K) finds the position straight away and doesn't have to rehash where K is the size of the key :complexity worst: O(K + N) when it has to rehash all items in the hash table where N is the table size position = self.__linear_probe (key, False) self.table[position] = None self.count -= 1 position = (position + 1) % len(self.table) while self.table[position] is not None: item = self.table[position] self.table[position] = None self.count -= 1 self[str(item [0])] = item[1] position = (position + 1) % len(self.table) def __rehash(self) -> None: Need to resize table and reinsert all values :complexity: new_hash = Linear ProbeHashTable (self.hash_base, LinearProbeHashTable. PRIMES[self.next_prime]) self.next_prime += 1 for i in range (len(self.table)): if self.table[i] is not None: new_hash(str(self.table[i][0])] = self.table[i][1] self.count = new_hash.count self. table = new_hash. table def __linear_probe (self, key: str, is_insert: bool) -> int: Find the correct position for this key in the hash table using linear probing :complexity best: O(K) first position is empty where K is the size of the key :complexity worst: O(K + N) when we've searched the entire table where N is the table_size :raises KeyError: When a position can't be found position = self.hash (key) # get the position using hash if is_insert and self.is_full(): raise KeyError(key) for in range (len (self.table)): # start traversing if self.table[position] is None: # found empty slot if is_insert: return position else: raise KeyError(key) # so the key is not in elif self.table[position][0] == key: # found key return position else: # there is something but not the key, try next position = (position + 1) % len(self.table) raise KeyError(key) def __contains__(self, key: str) -> bool: Checks to see if the given key is in the Hash Table see: #self.__getitem__(self, key: str) try: = self[key] except KeyError: return false else: return True def --getitem__(self, key: str) -> T: Get the item at a certain key :see: #self.__linear_probe (key: str, is_insert: bool) :raises KeyError: when the item doesn't exist position = self.__linear_probe (key, False) return self.table[position][1] def setitem__(self, key: str, data: 1) -> None: Set an (key, data) pair in our hash table see: #self.__linear_probe (key: str, is_insert: bool) :see: #self.__rehash() if self.is_full(): self.__rehash) position = self.__linear_probe (key, True) if self.table[position] is None: self.count += 1 self.table[position] = (key, data) def is_empty(self): Returns whether the hash table is empty :complexity: 0(1) return self.count == 0 def is_full(self): Returns whether the hash table is full :complexity: 0(1) return self.count == len(self.table) def hash(self, key: str) -> int: Universal Hash function post: returns a valid position (0 None: Utility method to call our setitem method :see: #__setitem__(self, key: str, data: T) self[key] = data def __str__(self) -> str: Returns all they key/value pairs in our hash table (no particular order) :complexity: 0(N) where N is the table size 24 25 26 27 08 29 20 1 2 3 24 result = " for item in self.table: if item is not None: (key, value) = item result += "(" + str(key) + return result + str(value) + ")
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


