Question: In the Exponential Growth Model (base e} if the growth rate is 2.75% (units day) how long does it take for the initial quantity to

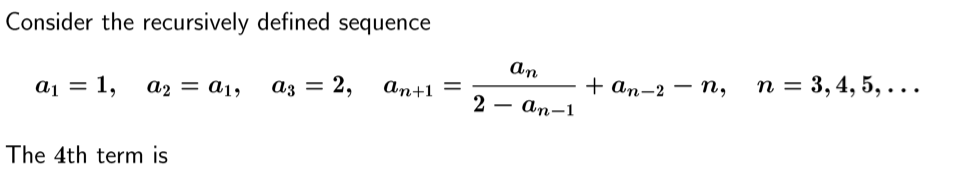
In the Exponential Growth Model (base e} if the growth rate is 2.75% (units day") how long does it take for the initial quantity to double? (Answer given to 2 d.p.) (A) 21.05 days (B) 0.25 days (C) 30.66 days (D) 25.21 days (E) 24.10 days Consider the recursively defined sequence an a1 = 1, a2 = a1, a3 = 2, and1 = + an-2 - n, n = 3, 4, 5,... 2 - an-1 The 4th term isThe 10th term of the sequence 9, 3, 1, -As 11 gets closer and closer to zero the function (1 + h gets closer and closer to

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Word Problem #14: The population of a town increased from 3650 people in the year 2007 to 4650 people in 2011. Find the absolute and relative (percent) increase. Absolute increase: ___ people...

The function f (z) = 12(6)" has been transformed to create function g (z) = 12(6)* How does the graph change from f (=) to g (I) O The graph will shift up 4 units. O The graph will shift left 4...

Solve the logarithmic equation for the unknown x. log2(3x - 1) + log2 8 = 5 X = Need Help? Read It Watch ItSolve the logarithmic equation for the unknown X. log4(x) = 10 Need Help? _' 3. [17.14...

In order to preserve the quality of topsoil, zucchini farmers are converting from synthetic fertilizers to using cover crops as mulch. In one region, originally 80,000 pounds of fertilizer was being...

subject: Differential Equations pls read instructions do not use ai. drop all references and link Instructions ODE application. - find an article related to ODE application - provide a short...

myopenmath.com Upgra MyOpen Get ne board Learn and Liv Instructor Test 2 2hrs14mins X Progress saved Sub Score: 6/15 6/15 answered Question 1 0/1 pt 9 3 0 Details The count in a bacteria culture was...

MATH019801-F22R-6943: HW 1.2 X + X C A ilearn.sfsu.edu/ay2223/mod/Iti/view.php?id=230696 R ... E iLearn Rafael Barajas Mendoza MATH019801-F22R- Question 5 0.8/1 pt ' 41-48 99 0 Details 6943...

2. [-/2 Points] SPRECALCS 4.6.008. ASK YOUR TEACHER PRACTICE ANOTHER It is observed that a certain bacteria culture has a relative growth rate of 19% per hour, but in the presence of an antibiotic...

Using the Rule of 70, estimate the time that it will take for a population to double if the growth rate is 1.3%. (*round to the nearest 10th of a year) Using the Rule of 70, estimate the the growth...

Consider the point (-1,-1) in the plane. OThere is only one way to represent this point in Cartesian coordinates: a = -1 and y = -1. OThere are many ways to represent this point in Cartesian...

Derive an expression in terms of land ml for the half-angle of the apex of the cone used to represent an angular momentum according to the vector model. Evaluate the expression for an ex spin. Show...

Question 1 5 ( 1 0 points ) Saved If the market price of a firm's output is correlated with its investment needs, the firm should a ) Underhedge, if at all, because it will have higher cashflows...

Complete the Following Columns. Input of Variable Factor Total Output or Product AP MP TFC AFC TVC AVC TC ATC MC 1 100 100 ---- 100 200 2 300 150 200 100 400 3 600 200 300 100 600 4 800 200 200 100...