In this assignment, your task is to optimize the cross sectional geometry of a Euler$-$Bernoulli beam to

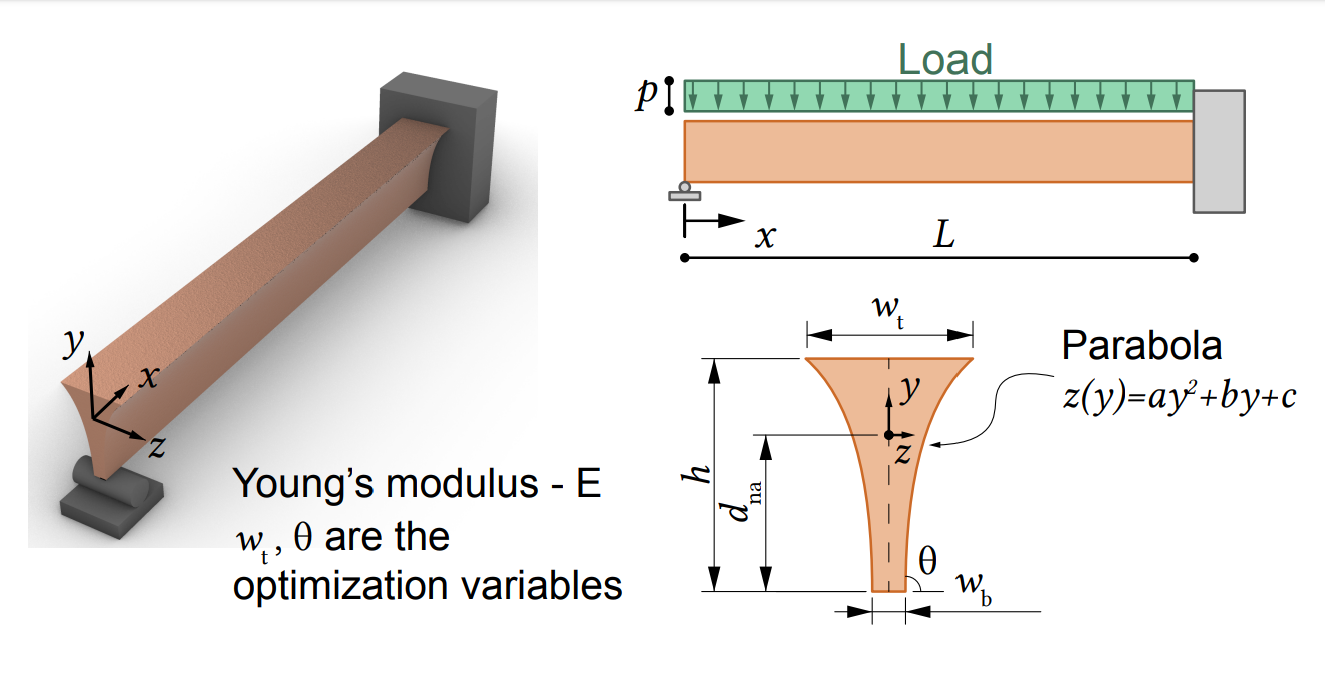
minimize its weight. The cross section is parabolic shaped with a height of h due to machining requirements.

If the vertical axis y is placed at the base of the cross section, then the top of the cross section at w$($y $=$ h$)=$ wt

is the widest. The base, y $=0,$ of the cross section is wb$.$ is the angle of inclination of the parabolic curve

that defines the side of the cross section.

A distributed load p is applied to the beam. The Youngs modulus of the material is E$,$ the yield strength

is y$,$ and the deflection is measured as u$($x$).$ We assume that h and wb are pre$-$defined, leaving and wt as

the optimization variables.

The manufacturer has set limits for the geometrical variables as follows: $0\mathrm{.}1$ wt $<mtext></mtext><mn>0</mn><mn>.</mn><mn>5</mn>$ and

For optimization, the yield strength of yield $=75$MPa, and the maximum deflection of L$/350$ should not be

exceeded.

Task $1-$ state ODE $(1$pt$)$

Write the governing ODE equation for Euler$-$Bernoulli beam.

Task $2-$ general solution $(1$pt$)$

Derive the general solution to the governing ODE, and calculate its derivatives.

Task $3-$ boundary conditions $(2$pt$)$

State the four boundary conditions according to the figure above.

Task $4-$ integration constants $(2$pt$)$

Solve for the integration constants of the ODE.

Task $5-$ define moment and axial stress $(2$pt$)$

Derive equations for moment and axial stress.

Task $6-$ Cross section $(3$pt$)$

State equations for the cross sectional area, A and second moment of area I. Begin by calculating the neutral

axis dna. Note that I is integrated from the bottom to the top of the cross section assuming y $=0$ at the dna.

Task $7-$ substitution $(2$pt$)$

Substitute the given constants into the above equations, so that in the end, A is a constant, u$($x$)$ depends

only on x and $\backslash$sigma depends only on x$,$ y$.$ Note this is for task $8$ and $9,$ where we want to plot the displacement

u$($x$)$ and $\backslash$sigma $($x$,$ y$)$ assuming wt and $\backslash$theta are given.

The parameters as as follows, E $=70$GPa, L $=20$m$,$ wt $=0\mathrm{.}25$m$,$ wt $=0\mathrm{.}02$m$,\backslash$theta $=0\mathrm{.}1,$ h $=0\mathrm{.}5$m$,$ p $=$

$5000$N$/$m$,\backslash$rho $=2700$kgm$3$

$,$ g $=9\mathrm{.}81$m$/$s

$2$

Task $8-$ plot displacement u$($x$)(1$pt$)$

plot u$($x$)$ as a function of x$.$ Use lambdify to convert symbolic functions to python functions.

Task $9-$ plot axial stress $\backslash$sigma $($x$,$ y$)(1$pt$)$

plot $\backslash$sigma $($x$,$ y$)$ as a function of x$,$ y$.$ Use lambdify to convert symbolic functions to python functions. Hint:

remember that y coordinate is defined w$.$r$.$t$.$ to the neutral axis dna.

Task $10-$ optimization $(2$pt$)$

Re$-$define your functions to replace x and y as constants, and take $\backslash$theta and wt as optimization variables.

Set x to where you think max displacement occur. Set x and y to where you think max stress occur $($is

it compressive or tensile$)?$

Task $11-$ contour plot $(2$pt$)$

Plot the optimization objective a filled contourf plot.

Draw the constraints as not$-$filled contour plot.

Find the optimal $\backslash$theta and wt by visually by looking for a minimum on this contour plot.

IF SOLVED CORRECT THEN I WILL GIVE YOU GOOD REVIEW.

Young's modulus $-$ EW$,,$ are theoptimization variableshLoadW,LWParabolazy$)=$ay$\text{'}+$by$+$c