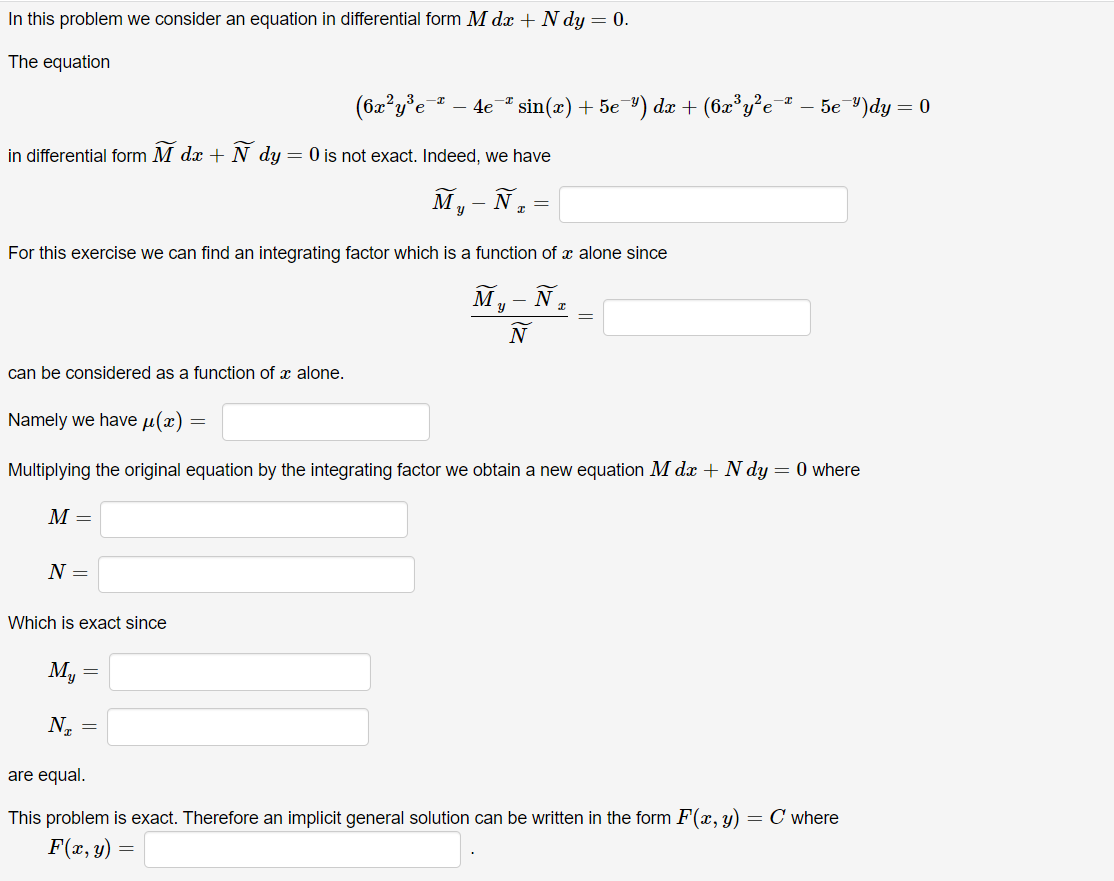
Question: In this problem we consider an equation in differential form Mdx+Ndy=0Mdx+Ndy=0.The equation in differential form Mdx+Ndy=0M~dx+N~dy=0 is not exact. Indeed, we have For this exercise
In this problem we consider an equation in differential form Mdx+Ndy=0Mdx+Ndy=0.The equation
in differential form Mdx+Ndy=0M~dx+N~dy=0 is not exact. Indeed, we have
For this exercise we can find an integrating factor which is a function of xx alone since
can be considered as a function of xx alone.Namely we have (x)=
Multiplying the original equation by the integrating factor we obtain a new equation Mdx+Ndy=0Mdx+Ndy=0 where
Which is exact since
My=My= Nx=Nx=
are equal.This problem is exact. Therefore an implicit general solution can be written in the form F(x,y)=CF(x,y)=C where
F(x,y)=F(x,y)=
In this problem we consider an equation in differential form Mdx+Ndy=0. The equation (6x2y3ex4exsin(x)+5ey)dx+(6x3y2ex5ey)dy=0 in differential form Mdx+Ndy=0 is not exact. Indeed, we have MyNx= For this exercise we can find an integrating factor which is a function of x alone since NMyNx= can be considered as a function of x alone. Namely we have (x)= Multiplying the original equation by the integrating factor we obtain a new equation Mdx+Ndy=0 where M=N= Which is exact since My=Nx= are equal. This problem is exact. Therefore an implicit general solution can be written in the form F(x,y)=C where F(x,y)=
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


