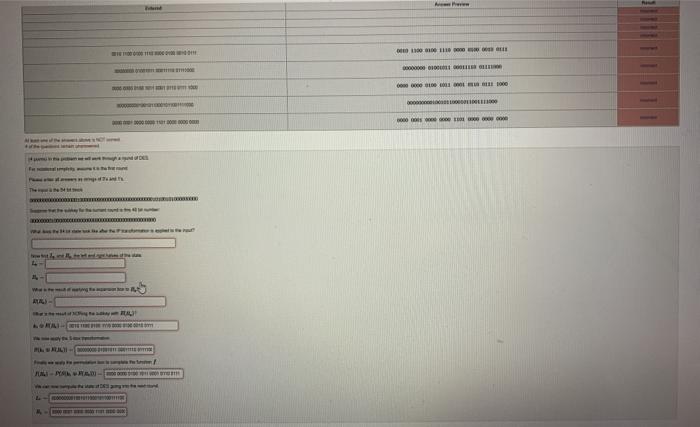
In this problem we will work through a round of DES.

For notational simplicity, assume it is the first round.

Please enter all answers as strings of 0's and 1's.

The input is the 64 bit block

00000000000000000010000000000000000000000000000101001010000000000000000000000000001000000000000000000000000000010100101000000000

Suppose that the subkey for the current round is this 48 bit number:

000000001000000000000000000000000000000000000000000000001000000000000000000000000000000000000000

What does the 64 bit state look like after the IP transformation is applied to the input?

Now find L0L0 and R0R0, the left and right halves of the state. L0=

R0=

What is the result of applying the expansion box to R0R0?

E(R0)=

What is the result of XORing the subkey with E(R0)E(R0)?

k1E(R0)=

We now apply the S-box transformation.

S(k1E(R0))=

Finally we apply the permutation box to complete the function ff.

f(R0)=P(S(k1E(R0)))=

We can now compute the state of DES going into the next round.

L1=

R1=

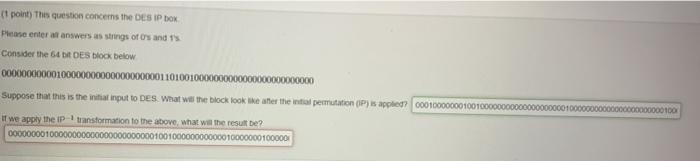
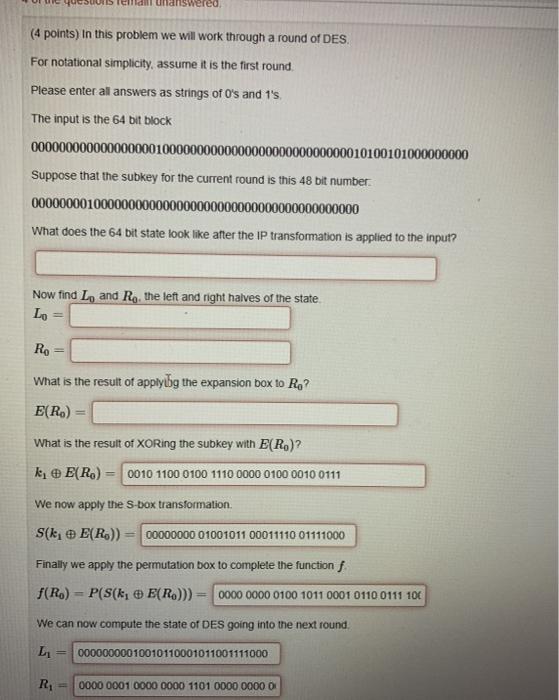
AISH --- GREGO - TOTO 1swered (4 points) In this problem we will work through a round of DES For notational simplicity, assume it is the first round Please enter all answers as strings of O's and 1's The input is the 64 bit block 0000000000000000001000000000000000000000000000010100101000000000 Suppose that the subkey for the current round is this 48 bit number 000000001000000000000000000000000000000000000000 What does the 64 bit state look like after the IP transformation is applied to the input? Now find L, and Ro the left and right halves of the state LO Ro What is the result of applyig the expansion box to R,? E(R.) What is the result of XORing the subkey with E(R)? k, E(R) = 0010 1100 0100 1110 0000 0100 0010 0111 We now apply the S-box transformation S(k, E(R)) = 00000000 01001011 00011110 01111000 Finally we apply the permutation box to complete the function f(Ro) - P(S(k, E(Ro))) = 0000 0000 0100 1011 0001 0110 0111 106 We can now compute the state of DES going into the next round L 00000000010010110001011001111000 R 0000 0001 0000 0000 1101 0000 0000 0 It point) This question concerns the DES IP BOX Please enter answers as strings of O's and 1 Consider the 64 DES block below 0000000000010000000000000000000011010010000000000000000000000000 Suppose that this is the initial input to DES. What will the block look teater the initial permutation (1P) is applied? 000100000001 0000000100 it we apply the transformation to the above what will the result be? 0000000010 100000000000010000000100000