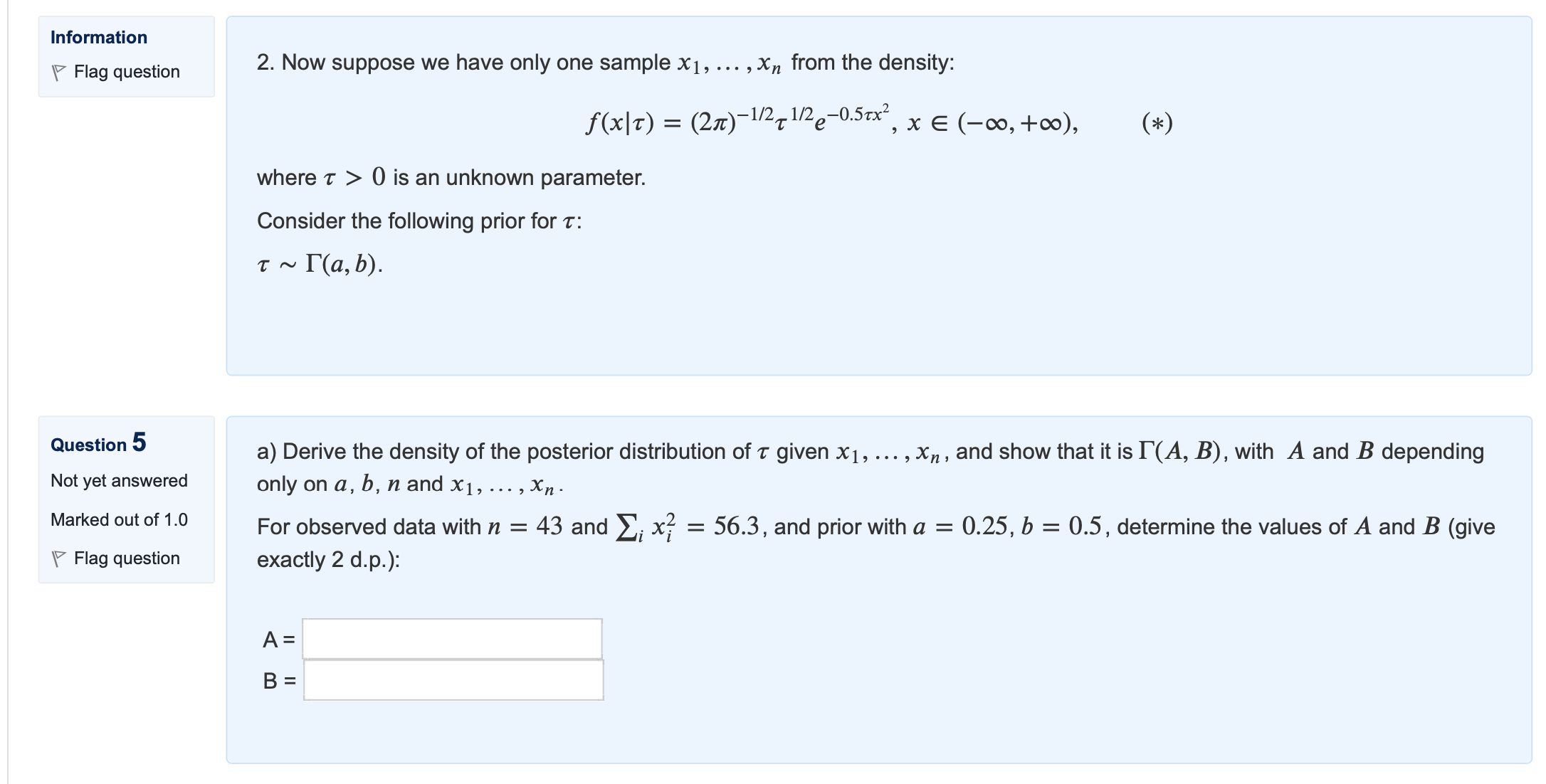
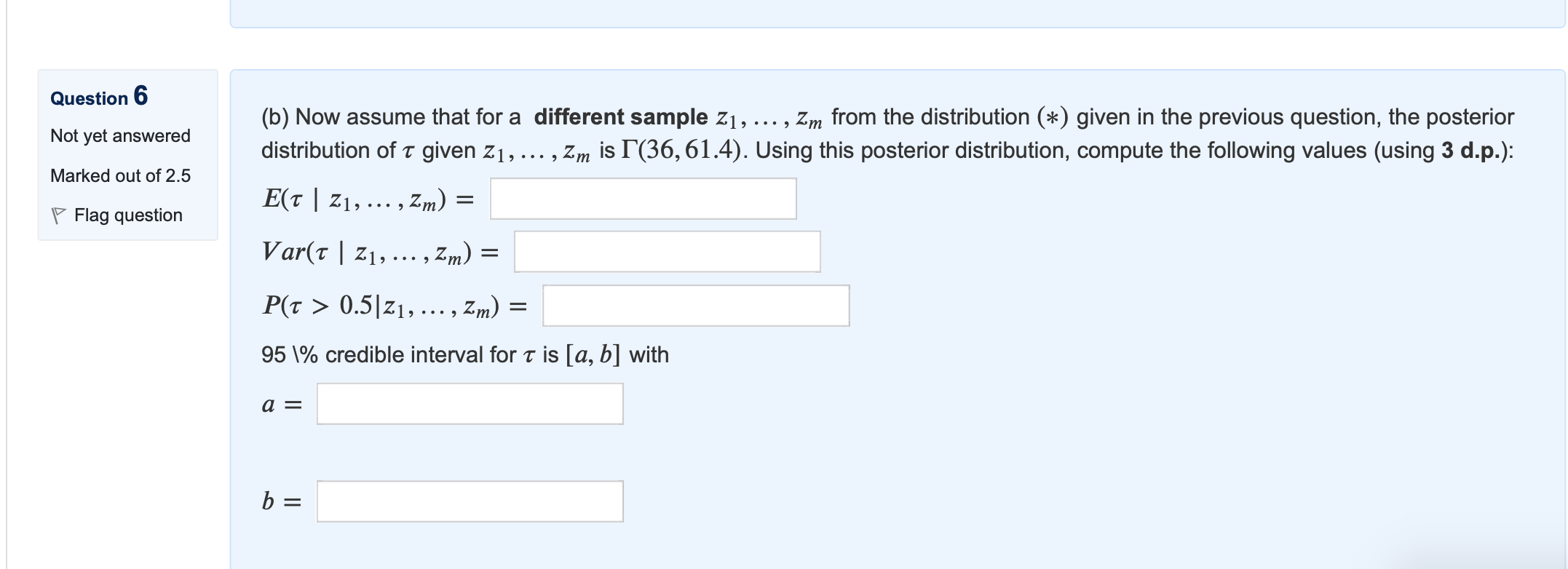
Information \\'7 Flag question Question 5 Not yet answered Marked out of 1.0 \\7 Flag question 2. Now suppose we have only one sample x1, , x,, from the density: f(x|1:) = (27r)'1/211/2e'0'5\"2, x E (oo,+oo), (*) where T > 0 is an unknown parameter. Consider the following prior for r: 7 ~ F(a, b). a) Derive the density of the posterior distribution OfT given x1, , X", and show that it is l"(A, B), with A and B depending only on a, b, nand x1, ,xn. For observed data with n = 43 and 2,. xi2 = 56.3, and prior with a = 0.25, b = 0.5, determine the values of A and B (give exactly 2 d.p.): Question 6 (b) Now assume that for a different sample Z1 , , Zn, from the distribution (*) given in the previous question. the posterior N t t d 0 ye answere distribution of 1' given 21 , ,2,\" is H36, 61.4). Using this posterior distribution, compute the following values (using 3 d.p.): Marked out of2.5 E(7 I Z1,... ,Zm) = \\'7 Flag question Var(1' | 21, ,2") = P(1 > 0.5|z1, ,zm) = 95 \\% credible interval for 1 is [a, b] with a