# Initialize variables

.data

v0: .float 2500.0

g: .float 32.174

range: .float 0.0

theta: .float 0.0

time_of_flight: .float 0.0

max_height: .float 0.0

yards: .float 3.0

deg: .float 180.0

cons: .float 2.0

cons2: .float 8.0

counter: .float 1.0

max_range: .float 42240.0

getrange: .asciiz "Enter range (in yards): "

tflight: .asciiz "Time of flight: "

hmax: .asciiz "Maximum height: "

angle: .asciiz "Angle trajectory: "

error: .asciiz "Error! Enter the range no more than 42240.0 yards "

newline: .asciiz " "

.text

main:

# Prompt user for range input

li $v0, 4

la $a0, getrange #range prompt

syscall

# Read user input for range

li $v0, 6

syscall

mov.s $f12, $f0 # store range in $f0 ($s0)

# Convert range from yards to feet

# lwc1 $f2, range #range in .data 1.0

lwc1 $f4, yards #yards conversion 3.0 in .data

mul.s $f2, $f0, $f4 #$f0 is the input multiply by 3.0($f4)

#valid input

#lwc1 $f11, max_range #f11 = 42240.0

#c.lt.s $f11, $f12 # if false check for next line $f12 = input, $f11 = 42240.0

#la $a0, newline

#li $v0, 4

#syscall

#la $a0, error #states error on display

#li $v0, 4

#syscall

#j main

# Calculate initial velocity

lwc1 $f0, v0

# Calculate time of flight and maximum height

jal sin_taylor # calculate angle using arcsin Taylor series

mov.s $f5, $f0 # store angle in $f5 ($s1)

lwc1 $f1, g #gravity 32.174

mul.s $f3, $f0, $f1 # calculate sin(theta) * g

lwc1 $f6, deg #load deg 180 in $f6 from .data

mul.s $f0, $f0, $f6 # convert angle to degrees

lwc1 $f7, cons #load constant float 2.0 from .data

mul.s $f1, $f1, $f7 # calculate 2 * g

mul.s $f2, $f2, $f5 # calculate v0 * sin(theta) *$s1 = $f5

div.s $f2, $f2, $f3 # calculate 2v0sin(theta)/g

swc1 $f2, time_of_flight # store time of flight

mul.s $f2, $f2, $f2 # calculate (2v0sin(theta)/g)^2

lwc1 $f8, cons2 #load 8.0 in float from .data in f8

div.s $f2, $f2, $f8 # calculate (2v0sin(theta)/g)^2 / 8

swc1 $f2, max_height # store maximum height

# Display results

#Angle trajectory

la $a0, angle

li $v0, 4

syscall

lwc1 $f12, theta

li $v0, 2

syscall

# print newline

li $v0, 4 # print string syscall

la $a0, newline

syscall

la $a0, tflight #time of flight message

li $v0, 4

syscall

lwc1 $f12, time_of_flight #final time of flight stored in time_of_flight

li $v0, 2

syscall

# print newline

li $v0, 4 # print string syscall

la $a0, newline

syscall

la $a0, hmax #print hmax initialization

li $v0, 4

syscall

lwc1 $f12, max_height #final maximum height stored in max_height

li $v0, 2

syscall

# Exit program

li $v0, 10

syscall

# Calculate arcsin using Taylor series

# $f0 - input

# $f1 - output

# $f9 - loop counter

sin_taylor:

#li $s0, 1 # set loop counter to 1

lwc1 $f9, counter #load 1.0 in floating to set loop counter to 1.

addi $sp, $sp, -8 # reserve space on stack for $f2 and $f3

swc1 $f1, 0($sp) # save $f1 on stack

swc1 $f0, 4($sp) # save $f0 on stack

lui $at, 0x3f80 # load 1.0 into $f2

mtc1 $zero, $f3 # initialize $f3 to 0.0

sin_taylor_loop:

div.s $f2, $f2, $f9 # calculate x^k / k!

mov.s $f10, $f9 # move loop counter to $t0 ($f10) for multiplication in floats *correct

mul.s $f3, $f3, $f0 # calculate (-1)^k * x^(2k+1)

mul.s $f3, $f3, $f2 # calculate (-1)^k * x^(2k+1) * x^k / k!

mul.s $f3, $f3, $f10 # calculate (-1)^k * x^(2k+1) * x^k / k! * k ----$f10 = $t0

addi $s0, $s0, 2 # increment loop counter by 2

ble $s0, 11, sin_taylor_loop # loop 6 times

# Final calculation for arcsin

addi $s0, $s0, -12 # subtract 12 from loop counter

mtc1 $zero, $f1 # initialize $f1 to 0.0

c.eq.s $f0, $f1 # check if input is 0

bc1f sin_taylor_end # if input is not 0, continue

lui $at, 0x3f80 # load 1.0 into $f1 #load upper immediate -- loads a register that is immediately available

mtc1 $at, $f1

b sin_taylor_end

sin_taylor_end:

addi $s0, $s0, -1 # decrement loop counter by 1

mul.s $f1, $f3, $f1 # calculate output

bgtz $s0, sin_taylor_end # loop until loop counter is 0

lwc1 $f0, 4($sp) # restore $f0 from stack

lwc1 $f1, 0($sp) # restore $f1 from stack

addi $sp, $sp, 8 # free space on stack

jr $ra

For the following code, use the following taylor series to find the arcsin and sin taylor series:

arcsin(x)=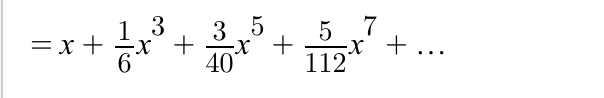

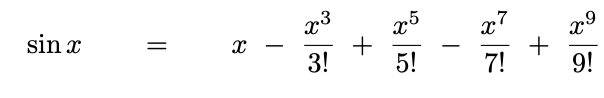
use the calculated angle to find the time of flight in seconds, maximum height in feet ; Please make sure that correct registers are used and everything works.

The assignment is to find the time of flight in seconds, maximum height in feet and angle trajectory in degrees from the input of range in yards while the maximum range is 42240 yards.

=x+61x3+403x5+1125x7+ sinx=x3!x3+5!x57!x7+9!x9