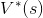is solution, and 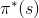is optimal policy

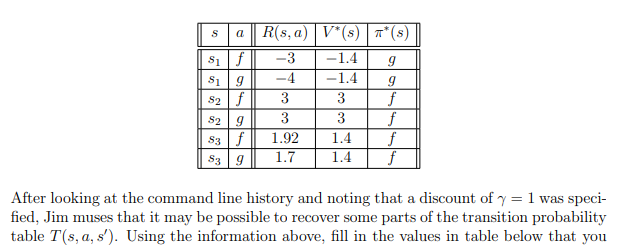
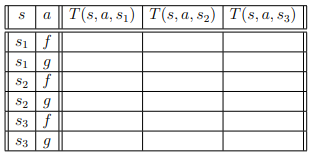
Recently, Jim has been working on building an intelligent agent to help a friend solve a problem that can be modeled using an MDP. In this environment, there are 3 possible states S = {S1, S2, S3} and at each state the agent always has 2 available actions A = {f,g}. Applying any action a from any state s has a probability T(s, a, s') of moving the agent to one of the other two states but will never result in the agent staying at the original state. The rewards for this environment represent the cost/reward of an action, and thus are only dependent on the original state and action taken (s' E S, R(s, a, s') = R(s, a)), not where the agent ended up. S a SS Si9 $2f S2 9 R(sa) V*(s)*(s) -3 -1.4 9 -4 -1.4 9 3 3 f 3 3 f 1.92 1.4 f 1.7 1.4 f $39 After looking at the command line history and noting that a discount of y = 1 was speci- fied, Jim muses that it may be possible to recover some parts of the transition probability table T(s, a, s'). Using the information above, fill in the values in table below that you can recover, writing a "X" in the cells that you cannot produce a value for. Show your work by explaining how you recovered the values in the box under the table. sa T(S, a, 81) T(s, a, 5) T(S, a, 52) T(, , $3) silf $19 $2f S29 S39 Recently, Jim has been working on building an intelligent agent to help a friend solve a problem that can be modeled using an MDP. In this environment, there are 3 possible states S = {S1, S2, S3} and at each state the agent always has 2 available actions A = {f,g}. Applying any action a from any state s has a probability T(s, a, s') of moving the agent to one of the other two states but will never result in the agent staying at the original state. The rewards for this environment represent the cost/reward of an action, and thus are only dependent on the original state and action taken (s' E S, R(s, a, s') = R(s, a)), not where the agent ended up. S a SS Si9 $2f S2 9 R(sa) V*(s)*(s) -3 -1.4 9 -4 -1.4 9 3 3 f 3 3 f 1.92 1.4 f 1.7 1.4 f $39 After looking at the command line history and noting that a discount of y = 1 was speci- fied, Jim muses that it may be possible to recover some parts of the transition probability table T(s, a, s'). Using the information above, fill in the values in table below that you can recover, writing a "X" in the cells that you cannot produce a value for. Show your work by explaining how you recovered the values in the box under the table. sa T(S, a, 81) T(s, a, 5) T(S, a, 52) T(, , $3) silf $19 $2f S29 S39