Is this the correct solution?

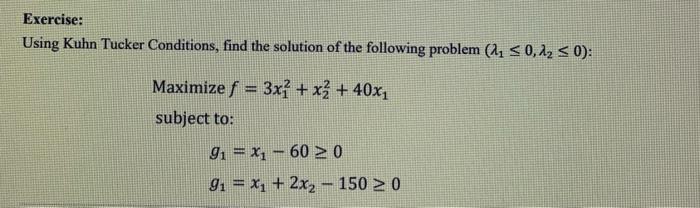
Using Kuhn Tucker Conditions, find the solution of the following problem (10,20) : Maximizef=3x12+x22+40x1subjectto:g1=x1600g1=x1+2x21500 To solve this problem using Kuhn-Tucker conditions, we first form the Lagrangian: L(x,)=312+x22+4011(x160)2(x1+22150) Then, we form the Kuhn-Tucker conditions: 1. Stationarity: L(x,)=61+4012=0 2. Primal feasibility: g1(x)=x1600g2(x)=x1+2x21500 3. Dual feasibility: 1020 4. Complementary slackness: 1g1(x)=02g2(x)=0 We can now solve for the optimal values of 1,2, and : From the stationarity condition, we have: 61+4012=0 From the complementary slackness conditions, we have: 1g1(x)=1(x160)=02g2(x)=2(x1+22150)=0 Therefore, we have three cases to consider: Case 1: 1=2=0 From the stationarity condition, we have: 61+40=01=20/3 From g1(x), we have: x16020/36000 This inequality is not satisfied, so this case is not feasible. Case2:1