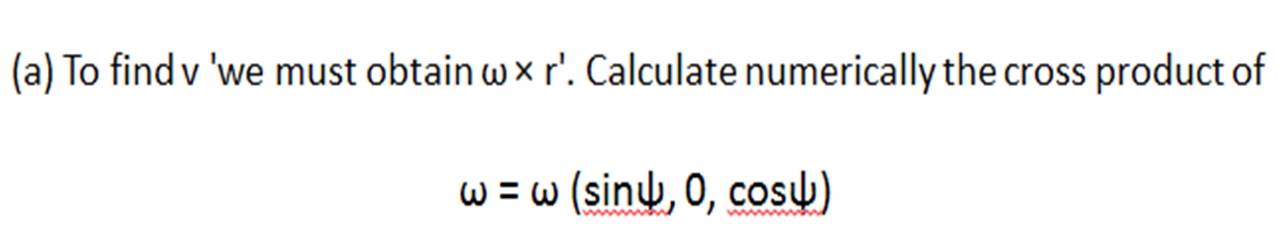
Just solve part a) Solve the following problem with MATLAB. Plot whatever is necessary. Show the program you made to graph and solve the problem. Magnetic ball. A spherical shell of radius R, carries a surface uniform charge o and rotates with an angular velocity w. We wish to find the vector magnetic potential at an arbitrary point r in space. For this, we first rotate our reference system such that the position r is on the z axis and that the angular velocity w is in the xz plane as seen in the image. w Y ' Figure 1: Rotating spherical shell with surface charge density o. Using the integral form of the potential vector on a surface K(r') A(r) 47 -DA'. (1) rd where K(r') is the surface current density given by K(r') = ov', while ra= VR2 + p2 2Rr cos O' and dA' = R2 sin O'd0'do'. (a) To find v 'we must obtain w x r'. Calculate numerically the cross product of w = w (sin, 0, cosy)) with r = R (sin O'cosa', sin sind', cos'). Just solve part a) Solve the following problem with MATLAB. Plot whatever is necessary. Show the program you made to graph and solve the problem. Magnetic ball. A spherical shell of radius R, carries a surface uniform charge o and rotates with an angular velocity w. We wish to find the vector magnetic potential at an arbitrary point r in space. For this, we first rotate our reference system such that the position r is on the z axis and that the angular velocity w is in the xz plane as seen in the image. w Y ' Figure 1: Rotating spherical shell with surface charge density o. Using the integral form of the potential vector on a surface K(r') A(r) 47 -DA'. (1) rd where K(r') is the surface current density given by K(r') = ov', while ra= VR2 + p2 2Rr cos O' and dA' = R2 sin O'd0'do'. (a) To find v 'we must obtain w x r'. Calculate numerically the cross product of w = w (sin, 0, cosy)) with r = R (sin O'cosa', sin sind', cos')